null hypothesis example sociology

Sociology 3112

Department of sociology, main navigation, hypothesis testing, learning objectives.

• Define and apply the various components of hypothesis testing, including: the null hypothesis, the research (or alternative) hypothesis, the test statistic and the critical statistic
• Understand the significance of rejecting/failing to reject the null hypothesis
• Carry out one- and two-group hypothesis tests

The null hypothesis (H0): a hypothesis that assumes there is no difference between the population parameters of the groups being tested. Under this assumption, any apparent difference between sample statistics is the result of sampling error. The research/alternative hypothesis (H1): a hypothesis that assumes the apparent difference between two sample statistics (or between a sample statistic and a population parameter) is due to actual differences in population parameters rather than sampling error. This hypothesis directly contradicts the null hypothesis (if the research hypothesis is true, the null must be false, and vice versa). Often researchers get excited when the research hypothesis proves to be correct. Alpha level (α): the level of probability at which the null hypothesis is rejected. In the social sciences, we usually set the alpha level at 0.05.

The t Distribution

The t Distribution is actually a series of distributions where the exact shape of each is determined by its respective degrees of freedom. The degrees of freedom represent the number of scores that are free to vary in calculating each statistic. For our purposes today, we can calculate the degrees of freedom by subtracting one from the total number of observations in each sample. So, the number of degrees of freedom will be nearly the same as the number of observations.

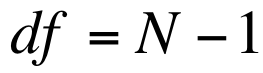
With few degrees of freedom, the t Distribution is very flat. As the degrees of freedom increase, the t Distribution looks more and more like the normal distribution. With 120+ degrees of freedom, it's indistinguishable from the normal distribution (and has all the same properties).

Hypothesis Testing and the t Distribution

This week we'll be talking about hypothesis tests as they apply to the means of two distributions. Sometimes that involves comparing a sample statistic to a population parameter (i.e., comparing the mean number of sexual partners in a sample of Sociology majors with the mean number of sexual partners of the entire student body), and sometimes it involves comparing the means of two samples (i.e., comparing the mean income of a sample of college graduates with the mean income of a sample of high school graduates). We can also do this for the proportions of two groups, but that process is slightly different than this one, so we will discuss it separately. What follows is a very general outline of hypothesis testing. For a more in-depth discussion, I highly recommend you read the chapter on hypothesis testing from David M. Lane's Online stats book.

Regardless of what we're testing, it's hard to be sure whether or not our data are indicative of a difference in the general population because of sampling error. In other words, the difference we're observing could have occurred simply by chance. In order to figure out just how unusual our results are, we run a hypothesis test. We often want our results to be unusual; the fact that the difference between two means (or two proportions) can't be explained by chance often means we've found some kind of noteworthy underlying pattern. There are lots of different kinds of hypothesis tests, but they all follow the same basic outline:

1. First we state our assumptions. There are certain criteria that need to be met before we can carry out a hypothesis test. These criteria will also determine which variety of hypothesis test we can use:

• Our sample must be randomly selected in order to minimize potential selection biases
• Our data must be interval/ratio (please don't try to carry out a t test on maleness or blackness or Mormon-ness)
• Our data must be normally distributed OR we must have a sample size of at least 50 for each group

2. Next we state our null/research hypotheses and set our alpha level.

• Our null hypothesis is always an equality, and it's usually the opposite of what we want to prove (some people like to think of it as being the status quo).
• Our research hypothesis is always an inequality, and it will determine what kind of test we use (i.e. one-tailed or two-tailed, which will be explained in more detail below).
• Our alpha level is our level of confidence for avoiding a Type One error. In other words, with an alpha of .05 (which is the most common in the social sciences), we're 95 percent sure we won't accidentally reject a true null hypothesis.

3. Third, we state our sampling distribution and our degrees of freedom and determine our critical statistic. Today, our sampling distribution is the difference between two means (i.e. the t Distribution) and our critical statistic is a t statistic. Playing with t statistics requires that we use a table not unlike the one for z statistics. Such a table is available on Canvas in the "Files" section. You'll note that the levels of significance are across the top and the degrees of freedom are along the side. The number that corresponds to a given level of significance and a certain number of degrees of freedom is what's known as a critical statistic. For example, the critical statistic for a one-tailed test with 60 degrees of freedom and an alpha of .05 is 1.671.

4. Fourth, we calculate our test statistic. We calculate a t-statistic in much the same way we would calculate a z statistic for a sampling distribution. The formulas for the one-group (comparing a sample mean to a population parameter) and two-group (comparing two sample means) hypothesis tests are as follows:

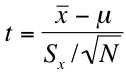
5. Finally, we accept or reject our null hypothesis. The absolute value of the obtained statistic must be larger than the critical statistic in order to reject the null hypothesis. We'll talk more about that below.

Hypothesis Testing with One Sample Mean

In this example, we're going to carry out a hypothesis test involving a single sample mean. In other words, we're going to see whether our sample mean is different from a known (or hypothesized) value. Let's say I'm testing a new diet drug that I believe dramatically increases weight loss. I know for a fact that the average person, via diet and exercise, will lose approximately two pounds per week. A sample of 100 people on my wonder drug, however, lost an average of three pounds per week with a standard deviation of one pound. Does my wonder drug work, or is the difference between my sample and the population entirely the result of sampling error?

First, we need to state our assumptions. Since this is my hypothetical example, it's safe to assume our data were randomly sampled. Weight (measured in pounds) is an interval/ratio variable, and we have a sample size greater than 50.

Next, we state our null and research hypothesis. Our null hypothesis is that my wonder drug doesn't work, and the mean of my sample is really no different from that of the population (in which case any apparent weight loss in the sample would have been due to dumb luck rather than the effectiveness of my wonder drug):

Our research hypothesis is that the drug does work, and the mean of my sample is greater than the mean of the population:

Because this research hypothesis specifies directionality (i.e. uses a "greater than" sign rather than a "not equal" sign), this will be a one-tailed test. For this test, let's set our alpha at 0.05. Now we calculate our t-statistic using the following formula:

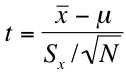
In other words, we subtract the known or hypothesized population mean from our sample mean and divide the result by the standard error of the mean. For the purposes of this problem, our equation would look like this:

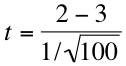
If we work that out, we get an obtained statistic of -10. When evaluating obtained against critical statistics, we're only interested in the absolute value of our obtained statistic. In order to make sense of that number, we need to compare it to the critical statistic from our table. First, however, we need to calculate our degrees of freedom, which are given by the formula N – 1 (100 – 1 = 99, so we have 99 degrees of freedom).

To use the table, find .05 in the "one-tail" line along the top of the table, and follow that column down to 99 degrees of freedom. You may notice at this point that 99 degrees of freedom is not included on our table. We have 80 and 100, but not 99. We want to get as close as we can without going over. With that in mind, we'd use the critical statistic found at 80 degrees of freedom, which is 1.664.

Finally, we compare our statistics and state our conclusion. If the absolute value of our obtained statistic is greater than the critical statistic, we can reject the null hypothesis. Because 10 is greater than 1.664 (the absolute value of -10 is 10), we can reject the null hypothesis and conclude that my wonder drug really works.

Hypothesis Testing with Two Sample Means

Now we're going to carry out a two-group hypothesis test using the following scores from a sample of men and women who took a standardized test:

Women: N = 41, Mean = 98, Standard Deviation = 8 Men: N = 21, Mean = 96.6, Standard Deviation = 12

Just from looking at the two sample means, we can see that women scored a little higher on this test than did men. But will that difference hold true for their respective populations, or is it due to sampling error? Let's find out.

First we state our assumptions. Since I'm giving you this example, I think it's safe to assume that the data was randomly selected and normally distributed. Test scores are definitely interval/ratio, so we can check that off as well.

Next, we state our null and research hypotheses and set our alpha level. Our null hypothesis is that the mean scores for the men and women who took this test are equal, so we would write something like this:

Our research hypothesis is that the means are not equal, so we would say:

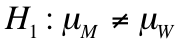
Because our research hypothesis is a simple inequality, we can run a two-tailed test. In other words, we don't care which mean is bigger than the other as long as they're not equal. If we wanted to prove that the mean score for women was higher than that of men, we would run a one-tailed test. As for our alpha level, we'll use 0.05 since it's usually the standard used in the social sciences.

Third, we state our sampling distribution, our degrees of freedom and calculate our critical statistic. We're testing the difference between two means, so our sampling distribution is the t distribution In this case our df is found by the equation (N-1)+(N-1), or 40 +20 = 60. If we find .05 (on the "two-tails" line) on the top of our table and follow that column down to the row that corresponds to 60 degrees of freedom, we see that the critical statistic is 2.000.

Fourth, we finally get to calculate our test statistic. The formula for calculating a t statistic is as follows:

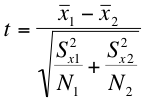
It's not as bad as it looks, I promise. If we plug in the means, variances and sample sizes of our example, it looks something like this:

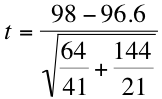
If we work that out, we get t = 1.4/2.9, which yields a t statistic of 0.48. But in order to make sense of that number, we need to compare it to our critical statistic, 2.000, which we can find on the cute little table your instructor gave you (see the end of Step 3 above for a more detailed explanation). Finally, we state our conclusion. Because our obtained t statistic (0.48) is smaller than the critical statistic (2.000), we accept the null hypothesis (or fail to reject the null hypothesis, as they say in the business) that the mean scores of men and women are the same. With a larger sample size, the standard error would have been smaller, so the t statistic would have been bigger and we would have had a better chance of rejecting the null hypothesis.

Main Points

• The t distribution is actually a family of distributions whose shapes vary according to their respective degrees of freedom, which is closely related to sample size.
• Hypothesis testing is a process by which we determine whether or not a sample result is likely to have occurred by chance. This process has five steps: (1) making assumptions (2) stating the null and research hypotheses and choosing an alpha level (3) selecting a sampling distribution and determining the test statistic that corresponds with the chosen alpha level (4) calculating the test statistic and (5) interpreting the results.
• We can use hypothesis tests to compare the mean of a sample to a known population mean (sometimes referred to as one-group hypothesis testing) and to compare two sample means (sometimes referred to as two-group hypothesis testing). Both types of hypothesis tests follow essentially the same process, but the formula used to calculate the test statistic differs between the two.

Hypothesis Testing in SPSS

To run a T-test in SPSS, click "Analyze," "Compare Means" and then "Independent-Samples T Test." The variable you want to test will go in the "Test Variable" space, and the "Grouping Variable" is how you define your two samples. For example, if you were testing the difference in income between men and women, income would go in the "Test Variable" box, and gender would go in the "Grouping Variable" box.

Once you have a variable to test in the "Test Variable" box and another in the "Grouping Variable" box, you'll need to click "Define Groups." (Note: the stage at which you define the groups you are going to test is where the vast majority of students get lost. So take your time with this next section.) Defining groups is necessary because T-tests can only handle two groups at once. If your grouping variable has more than two groups, you'll need to specify which two groups you would like to test. The "RACE" variable in the ADD Health dataset, for example, has five groups (White, African American, Native American, Asian/Pacific Islander and Other). If you wanted to use "RACE" as a grouping variable, you would need to tell SPSS which two groups to test (i.e., whites and African Americans, Native Americans and Others or maybe African Americans and Asians/Pacific Islanders—you get the idea). You cannot use a T-test to test all five groups at once.

Okay, now that we've got the "why" out of the way, lets move on to the "how." Suppose you wanted to use the ADD Health dataset to test for a difference in mean income between White and African American respondents. Many students begin by trying to type "White" into the "Group 1" box. When that doesn't work, they give up. Here's the thing: the "Group 1" and "Group 2" boxes will only accept numerical values. You need to enter the numbers that correspond to "White" and "African American." Go to the "Variable View" tab, and click on the "Value Labels" box for "RACE." You'll see that Whites were coded as ones and African Americans were coded as twos. That's what needs to go in the "Group 1" and "Group 2" boxes. So put a "1" for Whites in the "Group 1" box and a "2" for African Americans in the "Group 2" box and click "Continue." Similarly, if you wanted to test Whites and Asians/Pacific Islanders you would put a "1" in the "Group 1" box and a "4" in the "Group 2" box (Asians/Pacific Islanders were coded as fours). For an explanation of the SPSS output, I suggest you watch this video walkthrough:

• Using the NIS data, test for a difference in religious service attendance "ATTEND" between respondents who are married and those who have never been married (Hint: you'll need to check the value labels to see which number corresponds to each category). Report both the obtained statistic and the p-value. What is your conclusion? Does there appear to be a statistically significant difference?
• Using the same dataset, test for a difference in "EDUCATION" between men and women (Again, you'll need to check the value labels to see how males and females are coded). Report both the obtained statistic and the p-value. What is your conclusion? Does there appear to be a statistically significant difference?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 19098

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.

• The null hypothesis (\(H_{0}\)) is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
• The alternative hypothesis (\(H_{a}\)) is a claim about the population that is contradictory to \(H_{0}\) and what we conclude when we reject \(H_{0}\).

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data. After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_{0}\)" if the sample information favors the alternative hypothesis or "do not reject \(H_{0}\)" or "decline to reject \(H_{0}\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu_ 66\)
• \(H_{a}: \mu_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 66\)
• \(H_{a}: \mu < 66\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu_ 45\)
• \(H_{a}: \mu_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p_ 0.40\)
• \(H_{a}: p_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Contributors

• Template:ContribOpenStax

• Sociology Dictionary
• Books, Journals, Papers
• Guides & How To’s
• Life Around The World
• Research Methods
• Functionalism
• Postmodernism
• Social Constructionism
• Structuralism
• Symbolic Interactionism
• Sociology Theorists
• General Sociology
• Social Policy
• Social Work
• Sociology of Childhood
• Sociology of Crime & Deviance
• Sociology of Art
• Sociology of Dance
• Sociology of Food
• Sociology of Sport
• Sociology of Disability
• Sociology of Economics
• Sociology of Education
• Sociology of Emotion
• Sociology of Family & Relationships
• Sociology of Gender
• Sociology of Health
• Sociology of Identity
• Sociology of Ideology
• Sociology of Inequalities
• Sociology of Knowledge
• Sociology of Language
• Sociology of Law
• Sociology of Anime
• Sociology of Film
• Sociology of Gaming
• Sociology of Literature
• Sociology of Music
• Sociology of TV
• Sociology of Migration
• Sociology of Nature & Environment
• Sociology of Politics
• Sociology of Power
• Sociology of Race & Ethnicity
• Sociology of Religion
• Sociology of Sexuality
• Sociology of Social Movements
• Sociology of Technology
• Sociology of the Life Course
• Sociology of Travel & Tourism
• Sociology of Violence & Conflict
• Sociology of Work
• Urban Sociology
• Changing Relationships Within Families
• Conjugal Role Relationships
• Criticisms of Families
• Family Forms
• Functions of the Family
• Featured Articles
• Privacy Policy
• Terms & Conditions

What is a Hypothesis?

Table of Contents

Defining the hypothesis, the role of a hypothesis in the scientific method, types of hypotheses, hypothesis formulation, hypotheses and variables.

• The Importance of Testing Hypotheses
• The Hypothesis and Sociological Theory

In sociology, as in other scientific disciplines, the hypothesis serves as a crucial building block for research. It is a central element that directs the inquiry and provides a framework for testing the relationships between social phenomena. This article will explore what a hypothesis is, how it is formulated, and its role within the broader scientific method. By understanding the hypothesis, students of sociology can grasp how sociologists construct and test theories about the social world.

A hypothesis is a specific, testable statement about the relationship between two or more variables. It acts as a proposed explanation or prediction based on limited evidence, which researchers then test through empirical investigation. In essence, it is a statement that can be supported or refuted by data gathered from observation, experimentation, or other forms of systematic inquiry. The hypothesis typically takes the form of an “if-then” statement: if one variable changes, then another will change in response.

In sociological research, a hypothesis helps to focus the investigation by offering a clear proposition that can be tested. For instance, a sociologist might hypothesize that an increase in education levels leads to a decrease in crime rates. This hypothesis gives the researcher a direction, guiding them to collect data on education and crime, and analyze the relationship between the two variables. By doing so, the hypothesis serves as a tool for making sense of complex social phenomena.

The hypothesis is a key component of the scientific method, which is the systematic process by which sociologists and other scientists investigate the world. The scientific method begins with an observation of the world, followed by the formulation of a question or problem. Based on prior knowledge, theory, or preliminary observations, researchers then develop a hypothesis, which predicts an outcome or proposes a relationship between variables.

Once a hypothesis is established, researchers gather data to test it. If the data supports the hypothesis, it may be used to build a broader theory or to further refine the understanding of the social phenomenon in question. If the data contradicts the hypothesis, researchers may revise their hypothesis or abandon it altogether, depending on the strength of the evidence. In either case, the hypothesis helps to organize the research process, ensuring that it remains focused and methodologically sound.

In sociology, this method is particularly important because the social world is highly complex. Researchers must navigate a vast range of variables—age, gender, class, race, education, and countless others—that interact in unpredictable ways. A well-constructed hypothesis allows sociologists to narrow their focus to a manageable set of variables, making the investigation more precise and efficient.

Sociologists use different types of hypotheses, depending on the nature of their research question and the methods they plan to use. Broadly speaking, hypotheses can be classified into two main types: null hypotheses and alternative (or research) hypotheses.

Null Hypothesis

The null hypothesis, denoted as H0, states that there is no relationship between the variables being studied. It is a default assumption that any observed differences or relationships are due to random chance rather than a real underlying cause. In research, the null hypothesis serves as a point of comparison. Researchers collect data to see if the results allow them to reject the null hypothesis in favor of an alternative explanation.

For example, a sociologist studying the relationship between income and political participation might propose a null hypothesis that income has no effect on political participation. The goal of the research would then be to determine whether this null hypothesis can be rejected based on the data. If the data shows a significant correlation between income and political participation, the null hypothesis would be rejected.

Alternative Hypothesis

The alternative hypothesis, denoted as H1 or Ha, proposes that there is a significant relationship between the variables. This is the hypothesis that researchers aim to support with their data. In contrast to the null hypothesis, the alternative hypothesis predicts a specific direction or effect. For example, a researcher might hypothesize that higher levels of education lead to greater political engagement. In this case, the alternative hypothesis is proposing a positive correlation between the two variables.

The alternative hypothesis is the one that guides the research design, as it directs the researcher toward gathering evidence that will either support or refute the predicted relationship. The research process is structured around testing this hypothesis and determining whether the evidence is strong enough to reject the null hypothesis.

The process of formulating a hypothesis is both an art and a science. It requires a deep understanding of the social phenomena under investigation, as well as a clear sense of what is possible to observe and measure. Hypothesis formulation is closely linked to the theoretical framework that guides the research. Sociologists draw on existing theories to generate hypotheses, ensuring that their predictions are grounded in established knowledge.

To formulate a good hypothesis, a researcher must identify the key variables and determine how they are expected to relate to one another. Variables are the factors or characteristics that are being measured in a study. In sociology, these variables often include social attributes such as class, race, gender, age, education, and income, as well as behavioral variables like voting, criminal activity, or social participation.

For example, a sociologist studying the effects of social media on self-esteem might propose the following hypothesis: “Increased time spent on social media leads to lower levels of self-esteem among adolescents.” Here, the independent variable is the time spent on social media, and the dependent variable is the level of self-esteem. The hypothesis predicts a negative relationship between the two variables: as time spent on social media increases, self-esteem decreases.

A strong hypothesis has several key characteristics. It should be clear and specific, meaning that it unambiguously states the relationship between the variables. It should also be testable, meaning that it can be supported or refuted through empirical investigation. Finally, it should be grounded in theory, meaning that it is based on existing knowledge about the social phenomenon in question.

Membership Required

You must be a member to access this content.

View Membership Levels

Mr Edwards has a PhD in sociology and 10 years of experience in sociological knowledge

Related Articles

Fallacy of Composition

The fallacy of composition is a common logical error that occurs when one assumes that what is true for an...

The Role and Importance of Domain Assumptions in Sociology

Learn about domain assumption in sociology and its importance in sociological research. Understand the different types of domain assumptions and...

Social Constructionism: An Introduction

The Social Constructionist View of Femininity

What Are Signs?

Get the latest sociology.

How would you rate the content on Easy Sociology?

Recommended

Strain Theory and the LGBTQ+ Community

Representations of Masculinity in Conan the Barbarian Novels

24 hour trending.

Robert Merton’s Strain Theory Explained

The marxist view of the media, understanding conflict theories in sociology, pierre bourdieu’s symbolic violence: an outline and explanation, the british class system: an outline and explanation.

Easy Sociology makes sociology as easy as possible. Our aim is to make sociology accessible for everybody. © 2023 Easy Sociology

© 2023 Easy Sociology

• Science, Tech, Math ›
• Chemistry ›
• Scientific Method ›

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• What Are Examples of a Hypothesis?
• Random Error vs. Systematic Error
• Six Steps of the Scientific Method
• What Is a Hypothesis? (Science)
• Scientific Method Flow Chart
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Understanding Simple vs Controlled Experiments
• The Role of a Controlled Variable in an Experiment
• What Is an Experimental Constant?
• What Is a Testable Hypothesis?
• Scientific Hypothesis Examples
• What Is the Difference Between a Control Variable and Control Group?
• DRY MIX Experiment Variables Acronym
• What Is a Controlled Experiment?
• Scientific Variable

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

15 Null Hypothesis Examples

Chris Drew (PhD)

Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]

Learn about our Editorial Process

A null hypothesis is a general assertion or default position that there is no relationship or effect between two measured phenomena.

It’s a critical part of statistics, data analysis, and the scientific method . This concept forms the basis of testing statistical significance and allows researchers to be objective in their conclusions.

A null hypothesis helps to eliminate biases and ensures that the observed results are not due to chance. The rejection or failure to reject the null hypothesis helps in guiding the course of research.

Null Hypothesis Definition

The null hypothesis, often denoted as H 0 , is the hypothesis in a statistical test which proposes no statistical significance exists in a set of observed data.

It hypothesizes that any kind of difference or importance you see in a data set is due to chance.

Null hypotheses are typically proposed to be negated or disproved by statistical tests, paving way for the acceptance of an alternate hypothesis.

Importantly, a null hypothesis cannot be proven true; it can only be supported or rejected with confidence.

Should evidence – via statistical analysis – contradict the null hypothesis, it is rejected in favor of an alternative hypothesis. In essence, the null hypothesis is a tool to challenge and disprove that there is no effect or relationship between variables.

Video Explanation

I like to show this video to my students which outlines a null hypothesis really clearly and engagingly, using real life studies by research students! The into explains it really well:

“There’s an idea in science called the null hypothesis and it works like this: when you’re setting out to prove a theory, your default answer should be “it’s not going to work” and you have to convince the world otherwise through clear results”

Here’s the full video:

Null Hypothesis Examples

• Equality of Means: The null hypothesis posits that the average of group A does not differ from the average of group B. It suggests that any observed difference between the two group means is due to sampling or experimental error.
• No Correlation: The null hypothesis states there is no correlation between the variable X and variable Y in the population. It means that any correlation seen in sample data occurred by chance.
• Drug Effectiveness: The null hypothesis proposes that a new drug does not reduce the number of days to recover from a disease compared to a standard drug. Any observed difference is merely by chance and not due to the new drug.
• Classroom Teaching Method: The null hypothesis states that a new teaching method does not result in improved test scores compared to the traditional teaching method. Any improvement in scores can be attributed to chance or other unrelated factors.
• Smoking and Life Expectancy: The null hypothesis asserts that the average life expectancy of smokers is the same as that of non-smokers. Any perceived difference in life expectancy is due to random variation or other factors.
• Brand Preference: The null hypothesis suggests that the proportion of consumers preferring Brand A is the same as those preferring Brand B. Any observed preference in the sample is due to random selection.
• Vaccination Efficacy: The null hypothesis states that the efficacy of Vaccine A does not differ from that of Vaccine B. Any differences observed in a sample are due to chance or other confounding factors.
• Diet and Weight Loss: The null hypothesis proposes that following a specific diet does not result in more weight loss than not following the diet. Any weight loss observed among dieters is considered random or influenced by other factors.
• Exercise and Heart Rate: The null hypothesis states that regular exercise does not lower resting heart rate compared to no exercise. Any lower heart rates observed in exercisers could be due to chance or other unrelated factors.
• Climate Change: The null hypothesis asserts that the average global temperature this decade is not higher than the previous decade. Any observed temperature increase can be attributed to random variation or unaccounted factors.
• Gender Wage Gap: The null hypothesis posits that men and women earn the same average wage for the same job. Any observed wage disparity is due to chance or non-gender related factors.
• Psychotherapy Effectiveness: The null hypothesis states that patients undergoing psychotherapy do not show more improvement than those not undergoing therapy. Any improvement in the
• Energy Drink Consumption and Sleep: The null hypothesis proposes that consuming energy drinks does not affect the quantity of sleep. Any observed differences in sleep duration among energy drink consumers is due to random variation or other factors.
• Organic Food and Health: The null hypothesis asserts that consuming organic food does not lead to better health outcomes compared to consuming non-organic food. Any health differences observed in consumers of organic food are considered random or attributed to other confounding factors.
• Online Learning Effectiveness: The null hypothesis states that students learning online do not perform differently on exams than students learning in traditional classrooms. Any difference in performance can be attributed to chance or unrelated factors.

Null Hypothesis vs Alternative Hypothesis

An alternative hypothesis is the direct contrast to the null hypothesis. It posits that there is a statistically significant relationship or effect between the variables being observed.

If the null hypothesis is rejected based on the test data, the alternative hypothesis is accepted.

Importantly, while the null hypothesis is typically a statement of ‘no effect’ or ‘no difference,’ the alternative hypothesis states that there is an effect or difference.

Comprehension Checkpoint: How does the null hypothesis help to ensure that research is objective and unbiased?

Applications of the Null Hypothesis in Research

The null hypothesis plays a critical role in numerous research settings, promoting objectivity and ensuring findings aren’t due to random chance.

• Clinical Trials: Null hypothesis is used extensively in medical and pharmaceutical research. For example, when testing a new drug’s effectiveness, the null hypothesis might state that the drug has no effect on the disease. If data contradicts this, the null hypothesis is rejected, suggesting the drug might be effective.
• Business and Economics: Businesses use null hypotheses to make informed decisions. For instance, a company might use a null hypothesis to test if a new marketing strategy improves sales. If data suggests a significant increase in sales, the null hypothesis is rejected, and the new strategy may be implemented.
• Psychological Research: Psychologists use null hypotheses to test theories about behavior. For instance, a null hypothesis might state there’s no link between stress and sleep quality. Rejecting this hypothesis based on collected data could help establish a correlation between the two variables.
• Environmental Science: Null hypotheses are used to understand environmental changes. For instance, researchers might form a null hypothesis stating there is no significant difference in air quality before and after a policy change. If this hypothesis is rejected, it indicates the policy may have impacted air quality.
• Education: Educators and researchers often use null hypotheses to improve teaching methods. For example, a null hypothesis might propose a new teaching technique doesn’t enhance student performance. If data contradicts this, the technique may be beneficial.

In all these areas, the null hypothesis helps minimize bias, enabling researchers to support their findings with statistically significant data. It forms the backbone of many scientific research methodologies , promoting a disciplined approach to uncovering new knowledge.

See More Hypothesis Examples Here

The null hypothesis is a cornerstone of statistical analysis and empirical research. It serves as a starting point for investigations, providing a baseline premise that the observed effects are due to chance. By understanding and applying the concept of the null hypothesis, researchers can test the validity of their assumptions, making their findings more robust and reliable. In essence, the null hypothesis ensures that the scientific exploration remains objective, systematic, and free from unintended bias.

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 10 Reasons you’re Perpetually Single
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 20 Montessori Toddler Bedrooms (Design Inspiration)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 21 Montessori Homeschool Setups
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd-2/ 101 Hidden Talents Examples

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Open Education Sociology Dictionary

null hypothesis

Table of Contents

Definition of Null Hypothesis

( noun ) In statistical analysis , an hypothesis that predicts the absence of a relationship between two variables .

Example of Null Hypothesis

• “Education has no effect on mobility.”

Null Hypothesis Pronunciation

Pronunciation Usage Guide

Syllabification : null hy·poth·e·sis

Audio Pronunciation

Phonetic Spelling

• American English – /nUHl hie-pAHth-uh-suhs/
• British English – /nUHl hie-pOth-i-sis/

International Phonetic Alphabet

• American English – /nʌl haɪˈpɑθəsəs/
• British English – /nʌl haɪˈpɒθɪsɪs/

Usage Notes

• Plural: null hypotheses
• Note : The H is italicized .
• A null hypothesis can be true but still not discount the substantive hypothesis if it is low enough.

Additional Information

• Quantitative Research Resources – Books, Journals, and Helpful Links
• Word origin of “null” and “hypothesis” – Online Etymology Dictionary: etymonline.com

Related Terms

• control group
• correlation
• dependent variable
• descriptive statistics
• independent variable
• random sample
• reliability
• statistical analysis

Cite the Definition of Null Hypothesis

ASA – American Sociological Association (5th edition)

Bell, Kenton, ed. 2014. “null hypothesis.” In Open Education Sociology Dictionary . Retrieved December 4, 2024 ( https://sociologydictionary.org/null-hypothesis/ ).

APA – American Psychological Association (6th edition)

null hypothesis. (2014). In K. Bell (Ed.), Open education sociology dictionary . Retrieved from https://sociologydictionary.org/null-hypothesis/

Chicago/Turabian: Author-Date – Chicago Manual of Style (16th edition)

Bell, Kenton, ed. 2014. “null hypothesis.” In Open Education Sociology Dictionary . Accessed December 4, 2024. https://sociologydictionary.org/null-hypothesis/ .

MLA – Modern Language Association (7th edition)

“null hypothesis.” Open Education Sociology Dictionary . Ed. Kenton Bell. 2014. Web. 4 Dec. 2024. < https://sociologydictionary.org/null-hypothesis/ >.