sample hypothesis testing statements

15 Hypothesis Examples

Chris Drew (PhD)

Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]

Learn about our Editorial Process

A hypothesis is defined as a testable prediction , and is used primarily in scientific experiments as a potential or predicted outcome that scientists attempt to prove or disprove (Atkinson et al., 2021; Tan, 2022).

In my types of hypothesis article, I outlined 13 different hypotheses, including the directional hypothesis (which makes a prediction about an effect of a treatment will be positive or negative) and the associative hypothesis (which makes a prediction about the association between two variables).

This article will dive into some interesting examples of hypotheses and examine potential ways you might test each one.

Hypothesis Examples

1. “inadequate sleep decreases memory retention”.

Field: Psychology

Type: Causal Hypothesis A causal hypothesis explores the effect of one variable on another. This example posits that a lack of adequate sleep causes decreased memory retention. In other words, if you are not getting enough sleep, your ability to remember and recall information may suffer.

How to Test:

To test this hypothesis, you might devise an experiment whereby your participants are divided into two groups: one receives an average of 8 hours of sleep per night for a week, while the other gets less than the recommended sleep amount.

During this time, all participants would daily study and recall new, specific information. You’d then measure memory retention of this information for both groups using standard memory tests and compare the results.

Should the group with less sleep have statistically significant poorer memory scores, the hypothesis would be supported.

Ensuring the integrity of the experiment requires taking into account factors such as individual health differences, stress levels, and daily nutrition.

Relevant Study: Sleep loss, learning capacity and academic performance (Curcio, Ferrara & De Gennaro, 2006)

2. “Increase in Temperature Leads to Increase in Kinetic Energy”

Field: Physics

Type: Deductive Hypothesis The deductive hypothesis applies the logic of deductive reasoning – it moves from a general premise to a more specific conclusion. This specific hypothesis assumes that as temperature increases, the kinetic energy of particles also increases – that is, when you heat something up, its particles move around more rapidly.

This hypothesis could be examined by heating a gas in a controlled environment and capturing the movement of its particles as a function of temperature.

You’d gradually increase the temperature and measure the kinetic energy of the gas particles with each increment. If the kinetic energy consistently rises with the temperature, your hypothesis gets supporting evidence.

Variables such as pressure and volume of the gas would need to be held constant to ensure validity of results.

3. “Children Raised in Bilingual Homes Develop Better Cognitive Skills”

Field: Psychology/Linguistics

Type: Comparative Hypothesis The comparative hypothesis posits a difference between two or more groups based on certain variables. In this context, you might propose that children raised in bilingual homes have superior cognitive skills compared to those raised in monolingual homes.

Testing this hypothesis could involve identifying two groups of children: those raised in bilingual homes, and those raised in monolingual homes.

Cognitive skills in both groups would be evaluated using a standard cognitive ability test at different stages of development. The examination would be repeated over a significant time period for consistency.

If the group raised in bilingual homes persistently scores higher than the other, the hypothesis would thereby be supported.

The challenge for the researcher would be controlling for other variables that could impact cognitive development, such as socio-economic status, education level of parents, and parenting styles.

Relevant Study: The cognitive benefits of being bilingual (Marian & Shook, 2012)

4. “High-Fiber Diet Leads to Lower Incidences of Cardiovascular Diseases”

Field: Medicine/Nutrition

Type: Alternative Hypothesis The alternative hypothesis suggests an alternative to a null hypothesis. In this context, the implied null hypothesis could be that diet has no effect on cardiovascular health, which the alternative hypothesis contradicts by suggesting that a high-fiber diet leads to fewer instances of cardiovascular diseases.

To test this hypothesis, a longitudinal study could be conducted on two groups of participants; one adheres to a high-fiber diet, while the other follows a diet low in fiber.

After a fixed period, the cardiovascular health of participants in both groups could be analyzed and compared. If the group following a high-fiber diet has a lower number of recorded cases of cardiovascular diseases, it would provide evidence supporting the hypothesis.

Control measures should be implemented to exclude the influence of other lifestyle and genetic factors that contribute to cardiovascular health.

Relevant Study: Dietary fiber, inflammation, and cardiovascular disease (King, 2005)

5. “Gravity Influences the Directional Growth of Plants”

Field: Agronomy / Botany

Type: Explanatory Hypothesis An explanatory hypothesis attempts to explain a phenomenon. In this case, the hypothesis proposes that gravity affects how plants direct their growth – both above-ground (toward sunlight) and below-ground (towards water and other resources).

The testing could be conducted by growing plants in a rotating cylinder to create artificial gravity.

Observations on the direction of growth, over a specified period, can provide insights into the influencing factors. If plants consistently direct their growth in a manner that indicates the influence of gravitational pull, the hypothesis is substantiated.

It is crucial to ensure that other growth-influencing factors, such as light and water, are uniformly distributed so that only gravity influences the directional growth.

6. “The Implementation of Gamified Learning Improves Students’ Motivation”

Field: Education

Type: Relational Hypothesis The relational hypothesis describes the relation between two variables. Here, the hypothesis is that the implementation of gamified learning has a positive effect on the motivation of students.

To validate this proposition, two sets of classes could be compared: one that implements a learning approach with game-based elements, and another that follows a traditional learning approach.

The students’ motivation levels could be gauged by monitoring their engagement, performance, and feedback over a considerable timeframe.

If the students engaged in the gamified learning context present higher levels of motivation and achievement, the hypothesis would be supported.

Control measures ought to be put into place to account for individual differences, including prior knowledge and attitudes towards learning.

Relevant Study: Does educational gamification improve students’ motivation? (Chapman & Rich, 2018)

7. “Mathematics Anxiety Negatively Affects Performance”

Field: Educational Psychology

Type: Research Hypothesis The research hypothesis involves making a prediction that will be tested. In this case, the hypothesis proposes that a student’s anxiety about math can negatively influence their performance in math-related tasks.

To assess this hypothesis, researchers must first measure the mathematics anxiety levels of a sample of students using a validated instrument, such as the Mathematics Anxiety Rating Scale.

Then, the students’ performance in mathematics would be evaluated through standard testing. If there’s a negative correlation between the levels of math anxiety and math performance (meaning as anxiety increases, performance decreases), the hypothesis would be supported.

It would be crucial to control for relevant factors such as overall academic performance and previous mathematical achievement.

8. “Disruption of Natural Sleep Cycle Impairs Worker Productivity”

Field: Organizational Psychology

Type: Operational Hypothesis The operational hypothesis involves defining the variables in measurable terms. In this example, the hypothesis posits that disrupting the natural sleep cycle, for instance through shift work or irregular working hours, can lessen productivity among workers.

To test this hypothesis, you could collect data from workers who maintain regular working hours and those with irregular schedules.

Measuring productivity could involve examining the worker’s ability to complete tasks, the quality of their work, and their efficiency.

If workers with interrupted sleep cycles demonstrate lower productivity compared to those with regular sleep patterns, it would lend support to the hypothesis.

Consideration should be given to potential confounding variables such as job type, worker age, and overall health.

9. “Regular Physical Activity Reduces the Risk of Depression”

Field: Health Psychology

Type: Predictive Hypothesis A predictive hypothesis involves making a prediction about the outcome of a study based on the observed relationship between variables. In this case, it is hypothesized that individuals who engage in regular physical activity are less likely to suffer from depression.

Longitudinal studies would suit to test this hypothesis, tracking participants’ levels of physical activity and their mental health status over time.

The level of physical activity could be self-reported or monitored, while mental health status could be assessed using standard diagnostic tools or surveys.

If data analysis shows that participants maintaining regular physical activity have a lower incidence of depression, this would endorse the hypothesis.

However, care should be taken to control other lifestyle and behavioral factors that could intervene with the results.

Relevant Study: Regular physical exercise and its association with depression (Kim, 2022)

10. “Regular Meditation Enhances Emotional Stability”

Type: Empirical Hypothesis In the empirical hypothesis, predictions are based on amassed empirical evidence . This particular hypothesis theorizes that frequent meditation leads to improved emotional stability, resonating with numerous studies linking meditation to a variety of psychological benefits.

Earlier studies reported some correlations, but to test this hypothesis directly, you’d organize an experiment where one group meditates regularly over a set period while a control group doesn’t.

Both groups’ emotional stability levels would be measured at the start and end of the experiment using a validated emotional stability assessment.

If regular meditators display noticeable improvements in emotional stability compared to the control group, the hypothesis gains credit.

You’d have to ensure a similar emotional baseline for all participants at the start to avoid skewed results.

11. “Children Exposed to Reading at an Early Age Show Superior Academic Progress”

Type: Directional Hypothesis The directional hypothesis predicts the direction of an expected relationship between variables. Here, the hypothesis anticipates that early exposure to reading positively affects a child’s academic advancement.

A longitudinal study tracking children’s reading habits from an early age and their consequent academic performance could validate this hypothesis.

Parents could report their children’s exposure to reading at home, while standardized school exam results would provide a measure of academic achievement.

If the children exposed to early reading consistently perform better acadically, it gives weight to the hypothesis.

However, it would be important to control for variables that might impact academic performance, such as socioeconomic background, parental education level, and school quality.

12. “Adopting Energy-efficient Technologies Reduces Carbon Footprint of Industries”

Field: Environmental Science

Type: Descriptive Hypothesis A descriptive hypothesis predicts the existence of an association or pattern related to variables. In this scenario, the hypothesis suggests that industries adopting energy-efficient technologies will resultantly show a reduced carbon footprint.

Global industries making use of energy-efficient technologies could track their carbon emissions over time. At the same time, others not implementing such technologies continue their regular tracking.

After a defined time, the carbon emission data of both groups could be compared. If industries that adopted energy-efficient technologies demonstrate a notable reduction in their carbon footprints, the hypothesis would hold strong.

In the experiment, you would exclude variations brought by factors such as industry type, size, and location.

13. “Reduced Screen Time Improves Sleep Quality”

Type: Simple Hypothesis The simple hypothesis is a prediction about the relationship between two variables, excluding any other variables from consideration. This example posits that by reducing time spent on devices like smartphones and computers, an individual should experience improved sleep quality.

A sample group would need to reduce their daily screen time for a pre-determined period. Sleep quality before and after the reduction could be measured using self-report sleep diaries and objective measures like actigraphy, monitoring movement and wakefulness during sleep.

If the data shows that sleep quality improved post the screen time reduction, the hypothesis would be validated.

Other aspects affecting sleep quality, like caffeine intake, should be controlled during the experiment.

Relevant Study: Screen time use impacts low‐income preschool children’s sleep quality, tiredness, and ability to fall asleep (Waller et al., 2021)

14. Engaging in Brain-Training Games Improves Cognitive Functioning in Elderly

Field: Gerontology

Type: Inductive Hypothesis Inductive hypotheses are based on observations leading to broader generalizations and theories. In this context, the hypothesis deduces from observed instances that engaging in brain-training games can help improve cognitive functioning in the elderly.

A longitudinal study could be conducted where an experimental group of elderly people partakes in regular brain-training games.

Their cognitive functioning could be assessed at the start of the study and at regular intervals using standard neuropsychological tests.

If the group engaging in brain-training games shows better cognitive functioning scores over time compared to a control group not playing these games, the hypothesis would be supported.

15. Farming Practices Influence Soil Erosion Rates

Type: Null Hypothesis A null hypothesis is a negative statement assuming no relationship or difference between variables. The hypothesis in this context asserts there’s no effect of different farming practices on the rates of soil erosion.

Comparing soil erosion rates in areas with different farming practices over a considerable timeframe could help test this hypothesis.

If, statistically, the farming practices do not lead to differences in soil erosion rates, the null hypothesis is accepted.

However, if marked variation appears, the null hypothesis is rejected, meaning farming practices do influence soil erosion rates. It would be crucial to control for external factors like weather, soil type, and natural vegetation.

The variety of hypotheses mentioned above underscores the diversity of research constructs inherent in different fields, each with its unique purpose and way of testing.

While researchers may develop hypotheses primarily as tools to define and narrow the focus of the study, these hypotheses also serve as valuable guiding forces for the data collection and analysis procedures, making the research process more efficient and direction-focused.

Hypotheses serve as a compass for any form of academic research. The diverse examples provided, from Psychology to Educational Studies, Environmental Science to Gerontology, clearly demonstrate how certain hypotheses suit specific fields more aptly than others.

It is important to underline that although these varied hypotheses differ in their structure and methods of testing, each endorses the fundamental value of empiricism in research. Evidence-based decision making remains at the heart of scholarly inquiry, regardless of the research field, thus aligning all hypotheses to the core purpose of scientific investigation.

Testing hypotheses is an essential part of the scientific method . By doing so, researchers can either confirm their predictions, giving further validity to an existing theory, or they might uncover new insights that could potentially shift the field’s understanding of a particular phenomenon. In either case, hypotheses serve as the stepping stones for scientific exploration and discovery.

Atkinson, P., Delamont, S., Cernat, A., Sakshaug, J. W., & Williams, R. A. (2021).  SAGE research methods foundations . SAGE Publications Ltd.

Curcio, G., Ferrara, M., & De Gennaro, L. (2006). Sleep loss, learning capacity and academic performance.  Sleep medicine reviews ,  10 (5), 323-337.

Kim, J. H. (2022). Regular physical exercise and its association with depression: A population-based study short title: Exercise and depression.  Psychiatry Research ,  309 , 114406.

King, D. E. (2005). Dietary fiber, inflammation, and cardiovascular disease.  Molecular nutrition & food research ,  49 (6), 594-600.

Marian, V., & Shook, A. (2012, September). The cognitive benefits of being bilingual. In Cerebrum: the Dana forum on brain science (Vol. 2012). Dana Foundation.

Tan, W. C. K. (2022). Research Methods: A Practical Guide For Students And Researchers (Second Edition) . World Scientific Publishing Company.

Waller, N. A., Zhang, N., Cocci, A. H., D’Agostino, C., Wesolek‐Greenson, S., Wheelock, K., … & Resnicow, K. (2021). Screen time use impacts low‐income preschool children’s sleep quality, tiredness, and ability to fall asleep. Child: care, health and development, 47 (5), 618-626.

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ Free Social Skills Worksheets
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 10 Reasons you’re Perpetually Single
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 20 Montessori Toddler Bedrooms (Design Inspiration)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 21 Montessori Homeschool Setups

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.3 hypothesis testing examples.

• Example: Right-Tailed Test
• Example: Left-Tailed Test
• Example: Two-Tailed Test

Brinell Hardness Scores

An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:

The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:

H 0 : μ = 170 H A : μ > 170

The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

Descriptive Statistics

$\mu$: mean of Brinelli

Null hypothesis    H₀: $\mu$ = 170 Alternative hypothesis    H₁: $\mu$ > 170

The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.

If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):

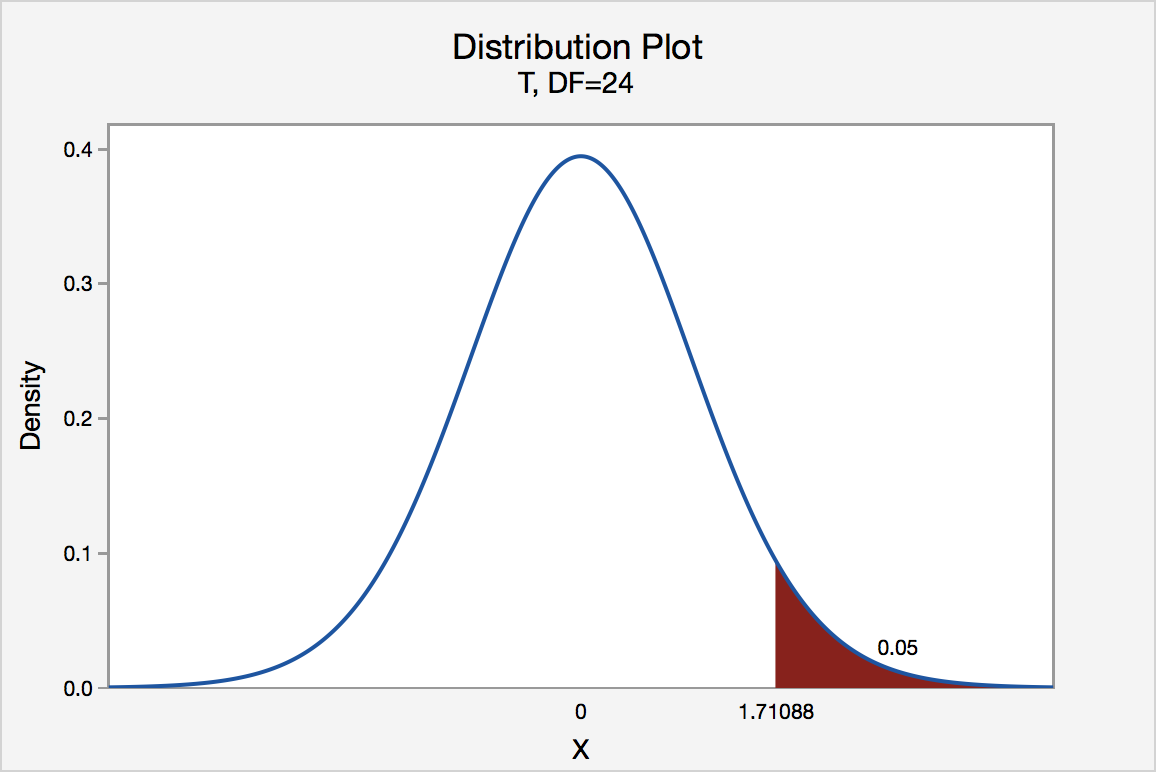
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:

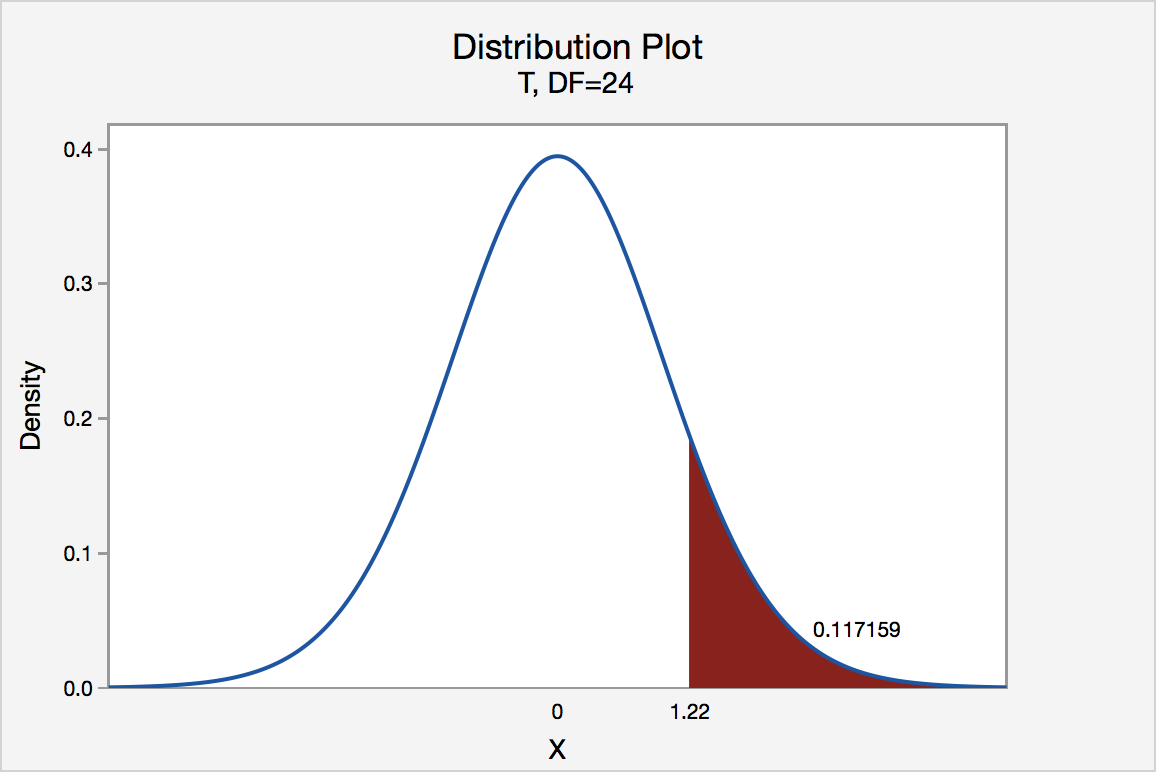
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than \(\alpha\) = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Height of Sunflowers

A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:

The biologist's hypotheses are:

H 0 : μ = 15.7 H A : μ < 15.7

The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:

$\mu$: mean of Height

Null hypothesis    H₀: $\mu$ = 15.7 Alternative hypothesis    H₁: $\mu$ < 15.7

The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.

Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."

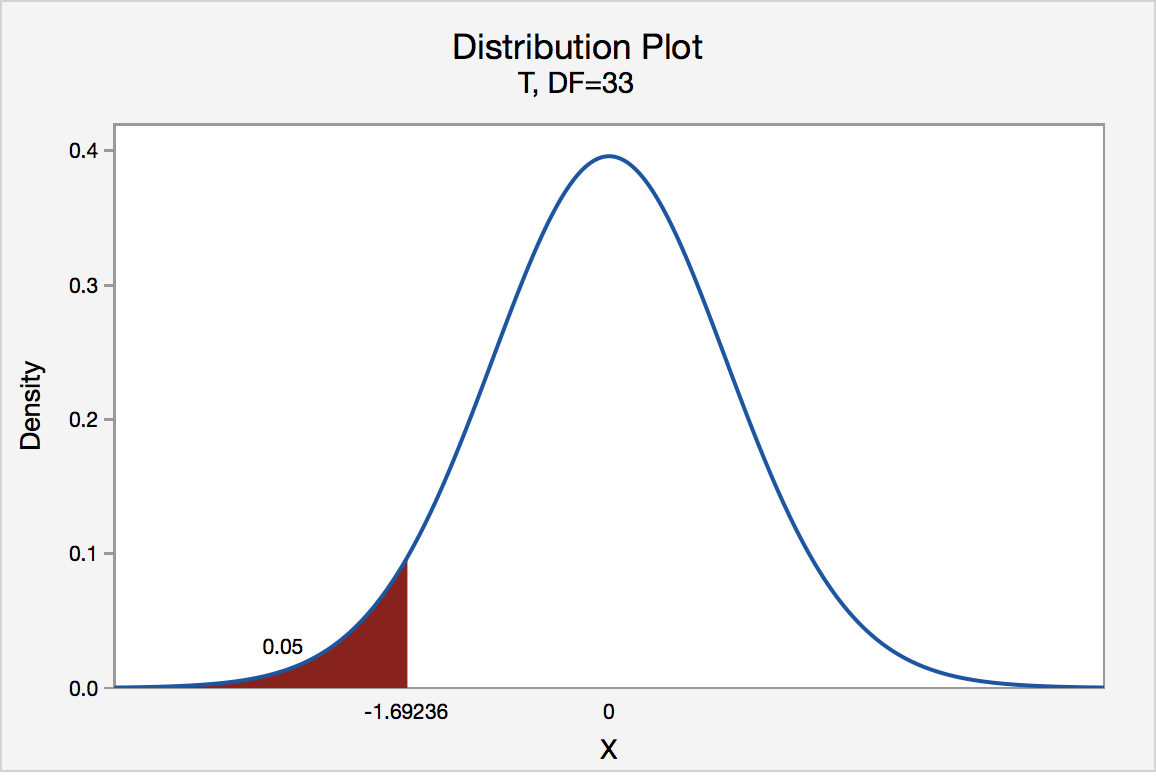
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3

Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:

In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than \(\alpha\) = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Gum Thickness

A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:

The quality control specialist's hypotheses are:

H 0 : μ = 7.5 H A : μ ≠ 7.5

The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

$\mu$: mean of Thickness

Null hypothesis    H₀: $\mu$ = 7.5 Alternative hypothesis    H₁: $\mu \ne$ 7.5

The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.

If the quality control specialist sets his significance level \(\alpha\) at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):

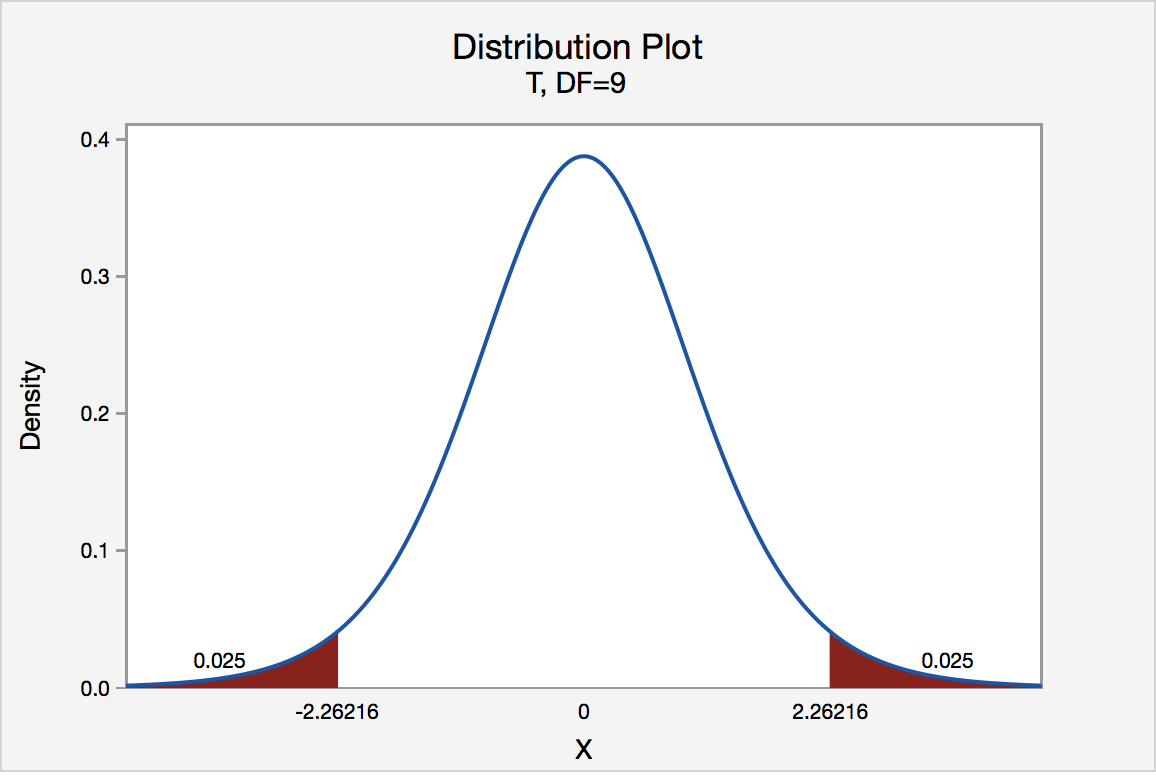
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.

If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:

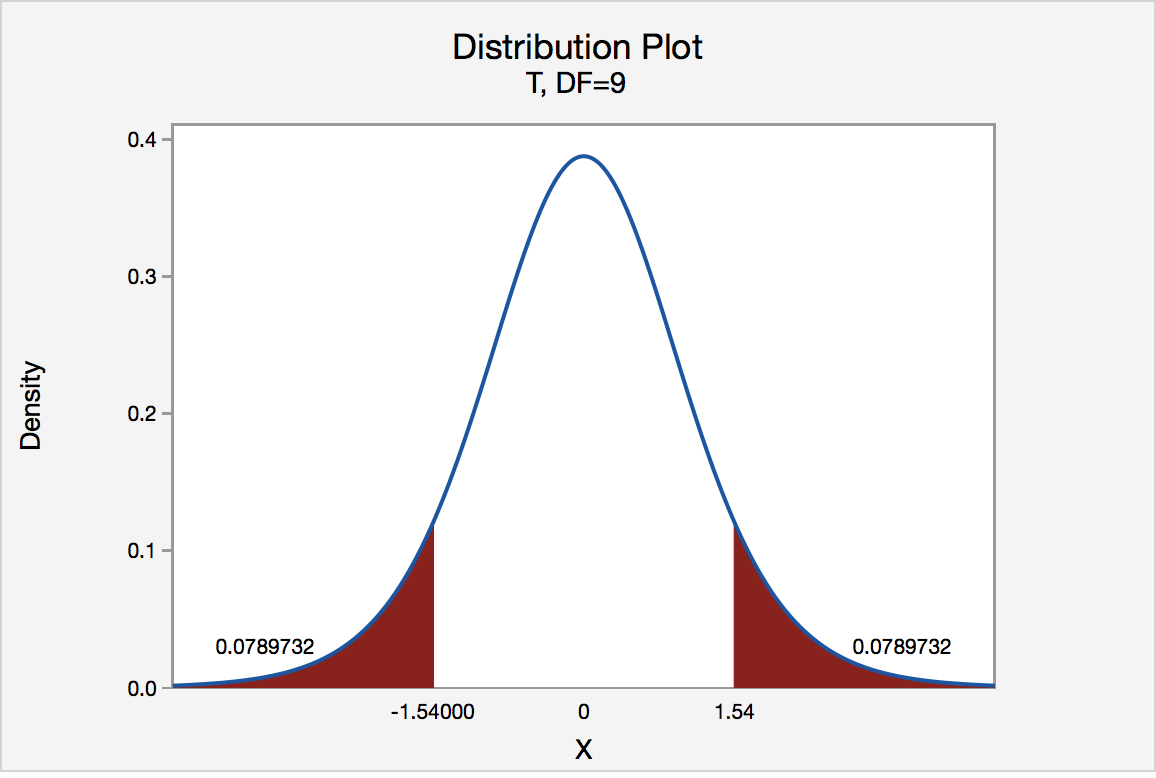
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than \(\alpha\) = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.

Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean \(\mu\). The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.

• How it works

"Christmas Offer"

Terms & conditions.

As the Christmas season is upon us, we find ourselves reflecting on the past year and those who we have helped to shape their future. It’s been quite a year for us all! The end of the year brings no greater joy than the opportunity to express to you Christmas greetings and good wishes.

At this special time of year, Research Prospect brings joyful discount of 10% on all its services. May your Christmas and New Year be filled with joy.

We are looking back with appreciation for your loyalty and looking forward to moving into the New Year together.

"Claim this offer"

In unfamiliar and hard times, we have stuck by you. This Christmas, Research Prospect brings you all the joy with exciting discount of 10% on all its services.

Offer valid till 5-1-2024

We love being your partner in success. We know you have been working hard lately, take a break this holiday season to spend time with your loved ones while we make sure you succeed in your academics

Discount code: RP0996Y

Hypothesis Testing – A Complete Guide with Examples

Published by Alvin Nicolas at August 14th, 2021 , Revised On October 26, 2023

In statistics, hypothesis testing is a critical tool. It allows us to make informed decisions about populations based on sample data. Whether you are a researcher trying to prove a scientific point, a marketer analysing A/B test results, or a manufacturer ensuring quality control, hypothesis testing plays a pivotal role. This guide aims to introduce you to the concept and walk you through real-world examples.

What is a Hypothesis and a Hypothesis Testing?

A hypothesis is considered a belief or assumption that has to be accepted, rejected, proved or disproved. In contrast, a research hypothesis is a research question for a researcher that has to be proven correct or incorrect through investigation.

What is Hypothesis Testing?

Hypothesis testing  is a scientific method used for making a decision and drawing conclusions by using a statistical approach. It is used to suggest new ideas by testing theories to know whether or not the sample data supports research. A research hypothesis is a predictive statement that has to be tested using scientific methods that join an independent variable to a dependent variable.  

Example: The academic performance of student A is better than student B

Characteristics of the Hypothesis to be Tested

A hypothesis should be:

• Clear and precise
• Capable of being tested
• Able to relate to a variable
• Stated in simple terms
• Consistent with known facts
• Limited in scope and specific
• Tested in a limited timeframe
• Explain the facts in detail

What is a Null Hypothesis and Alternative Hypothesis?

A  null hypothesis  is a hypothesis when there is no significant relationship between the dependent and the participants’ independent  variables . 

In simple words, it’s a hypothesis that has been put forth but hasn’t been proved as yet. A researcher aims to disprove the theory. The abbreviation “Ho” is used to denote a null hypothesis.

If you want to compare two methods and assume that both methods are equally good, this assumption is considered the null hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is similar to the previous model of the car, on average. You can write it as: Ho: there is no difference between the mileage of both vehicles. If your findings don’t support your hypothesis and you get opposite results, this outcome will be considered an alternative hypothesis.

If you assume that one method is better than another method, then it’s considered an alternative hypothesis. The alternative hypothesis is the theory that a researcher seeks to prove and is typically denoted by H1 or HA.

If you support a null hypothesis, it means you’re not supporting the alternative hypothesis. Similarly, if you reject a null hypothesis, it means you are recommending the alternative hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is better than the previous model of the vehicle. You can write it as; Ha: the two vehicles have different mileage. On average/ the fuel consumption of the new vehicle model is better than the previous model.

If a null hypothesis is rejected during the hypothesis test, even if it’s true, then it is considered as a type-I error. On the other hand, if you don’t dismiss a hypothesis, even if it’s false because you could not identify its falseness, it’s considered a type-II error.

Hire an Expert Researcher

Orders completed by our expert writers are

• Formally drafted in academic style
• 100% Plagiarism free & 100% Confidential
• Never resold
• Include unlimited free revisions
• Completed to match exact client requirements

How to Conduct Hypothesis Testing?

Here is a step-by-step guide on how to conduct hypothesis testing.

Step 1: State the Null and Alternative Hypothesis

Once you develop a research hypothesis, it’s important to state it is as a Null hypothesis (Ho) and an Alternative hypothesis (Ha) to test it statistically.

A null hypothesis is a preferred choice as it provides the opportunity to test the theory. In contrast, you can accept the alternative hypothesis when the null hypothesis has been rejected.

Example: You want to identify a relationship between obesity of men and women and the modern living style. You develop a hypothesis that women, on average, gain weight quickly compared to men. Then you write it as: Ho: Women, on average, don’t gain weight quickly compared to men. Ha: Women, on average, gain weight quickly compared to men.

Step 2: Data Collection

Hypothesis testing follows the statistical method, and statistics are all about data. It’s challenging to gather complete information about a specific population you want to study. You need to  gather the data  obtained through a large number of samples from a specific population. 

Example: Suppose you want to test the difference in the rate of obesity between men and women. You should include an equal number of men and women in your sample. Then investigate various aspects such as their lifestyle, eating patterns and profession, and any other variables that may influence average weight. You should also determine your study’s scope, whether it applies to a specific group of population or worldwide population. You can use available information from various places, countries, and regions.

Step 3: Select Appropriate Statistical Test

There are many  types of statistical tests , but we discuss the most two common types below, such as One-sided and two-sided tests.

Note: Your choice of the type of test depends on the purpose of your study 

One-sided Test

In the one-sided test, the values of rejecting a null hypothesis are located in one tail of the probability distribution. The set of values is less or higher than the critical value of the test. It is also called a one-tailed test of significance.

Example: If you want to test that all mangoes in a basket are ripe. You can write it as: Ho: All mangoes in the basket, on average, are ripe. If you find all ripe mangoes in the basket, the null hypothesis you developed will be true.

Two-sided Test

In the two-sided test, the values of rejecting a null hypothesis are located on both tails of the probability distribution. The set of values is less or higher than the first critical value of the test and higher than the second critical value test. It is also called a two-tailed test of significance. 

Example: Nothing can be explicitly said whether all mangoes are ripe in the basket. If you reject the null hypothesis (Ho: All mangoes in the basket, on average, are ripe), then it means all mangoes in the basket are not likely to be ripe. A few mangoes could be raw as well.

Get statistical analysis help at an affordable price

• An expert statistician will complete your work
• Rigorous quality checks
• Confidentiality and reliability
• Any statistical software of your choice
• Free Plagiarism Report

Step 4: Select the Level of Significance

When you reject a null hypothesis, even if it’s true during a statistical hypothesis, it is considered the  significance level . It is the probability of a type one error. The significance should be as minimum as possible to avoid the type-I error, which is considered severe and should be avoided. 

If the significance level is minimum, then it prevents the researchers from false claims. 

The significance level is denoted by  P,  and it has given the value of 0.05 (P=0.05)

If the P-Value is less than 0.05, then the difference will be significant. If the P-value is higher than 0.05, then the difference is non-significant.

Example: Suppose you apply a one-sided test to test whether women gain weight quickly compared to men. You get to know about the average weight between men and women and the factors promoting weight gain.

Step 5: Find out Whether the Null Hypothesis is Rejected or Supported

After conducting a statistical test, you should identify whether your null hypothesis is rejected or accepted based on the test results. It would help if you observed the P-value for this.

Example: If you find the P-value of your test is less than 0.5/5%, then you need to reject your null hypothesis (Ho: Women, on average, don’t gain weight quickly compared to men). On the other hand, if a null hypothesis is rejected, then it means the alternative hypothesis might be true (Ha: Women, on average, gain weight quickly compared to men. If you find your test’s P-value is above 0.5/5%, then it means your null hypothesis is true.

Step 6: Present the Outcomes of your Study

The final step is to present the  outcomes of your study . You need to ensure whether you have met the objectives of your research or not. 

In the discussion section and  conclusion , you can present your findings by using supporting evidence and conclude whether your null hypothesis was rejected or supported.

In the result section, you can summarise your study’s outcomes, including the average difference and P-value of the two groups.

If we talk about the findings, our study your results will be as follows:

Example: In the study of identifying whether women gain weight quickly compared to men, we found the P-value is less than 0.5. Hence, we can reject the null hypothesis (Ho: Women, on average, don’t gain weight quickly than men) and conclude that women may likely gain weight quickly than men.

Did you know in your academic paper you should not mention whether you have accepted or rejected the null hypothesis? 

Always remember that you either conclude to reject Ho in favor of Haor   do not reject Ho . It would help if you never rejected  Ha  or even  accept Ha .

Suppose your null hypothesis is rejected in the hypothesis testing. If you conclude  reject Ho in favor of Haor   do not reject Ho,  then it doesn’t mean that the null hypothesis is true. It only means that there is a lack of evidence against Ho in favour of Ha. If your null hypothesis is not true, then the alternative hypothesis is likely to be true.

Example: We found that the P-value is less than 0.5. Hence, we can conclude reject Ho in favour of Ha (Ho: Women, on average, don’t gain weight quickly than men) reject Ho in favour of Ha. However, rejected in favour of Ha means (Ha: women may likely to gain weight quickly than men)

Frequently Asked Questions

What are the 3 types of hypothesis test.

The 3 types of hypothesis tests are:

• One-Sample Test : Compare sample data to a known population value.
• Two-Sample Test : Compare means between two sample groups.
• ANOVA : Analyze variance among multiple groups to determine significant differences.

What is a hypothesis?

A hypothesis is a proposed explanation or prediction about a phenomenon, often based on observations. It serves as a starting point for research or experimentation, providing a testable statement that can either be supported or refuted through data and analysis. In essence, it’s an educated guess that drives scientific inquiry.

What are null hypothesis?

A null hypothesis (often denoted as H0) suggests that there is no effect or difference in a study or experiment. It represents a default position or status quo. Statistical tests evaluate data to determine if there’s enough evidence to reject this null hypothesis.

What is the probability value?

The probability value, or p-value, is a measure used in statistics to determine the significance of an observed effect. It indicates the probability of obtaining the observed results, or more extreme, if the null hypothesis were true. A small p-value (typically <0.05) suggests evidence against the null hypothesis, warranting its rejection.

What is p value?

The p-value is a fundamental concept in statistical hypothesis testing. It represents the probability of observing a test statistic as extreme, or more so, than the one calculated from sample data, assuming the null hypothesis is true. A low p-value suggests evidence against the null, possibly justifying its rejection.

What is a t test?

A t-test is a statistical test used to compare the means of two groups. It determines if observed differences between the groups are statistically significant or if they likely occurred by chance. Commonly applied in research, there are different t-tests, including independent, paired, and one-sample, tailored to various data scenarios.

When to reject null hypothesis?

Reject the null hypothesis when the test statistic falls into a predefined rejection region or when the p-value is less than the chosen significance level (commonly 0.05). This suggests that the observed data is unlikely under the null hypothesis, indicating evidence for the alternative hypothesis. Always consider the study’s context.

You May Also Like

Experimental research refers to the experiments conducted in the laboratory or under observation in controlled conditions. Here is all you need to know about experimental research.

A confounding variable can potentially affect both the suspected cause and the suspected effect. Here is all you need to know about accounting for confounding variables in research.

Thematic analysis is commonly used for qualitative data. Researchers give preference to thematic analysis when analysing audio or video transcripts.

As Featured On

USEFUL LINKS

LEARNING RESOURCES

COMPANY DETAILS

Splash Sol LLC

• How It Works

Testing Hypothesis Statement

Ai generator.

In the intricate dance of scientific research, forming a testable hypothesis is the linchpin. It’s more than just a guess—it’s a precise, verifiable prediction awaiting experimentation. To ensure accuracy and validity, crafting a powerful hypothesis thesis statement is crucial. Delve into our curated examples, insightful writing guides, and practical tips to master the art of creating hypotheses that can effectively steer your research journey. Dive in and prepare to experiment with confidence!

What is a Testing/ Test/ Testable Thesis Statement? – Definition

A testing or testable thesis statement, much like a scientific hypothesis, is a specific, clear, and focused assertion that can be proven or disproven through empirical means, such as experiments, observations, or data collection and analysis. Unlike broad or opinion-based hypothesis statements , a testable thesis statement sets the stage for empirical research by posing a claim or prediction that can be evaluated through evidence-based methodologies.

What is an example of a Testing thesis statement?

Example: In the context of botany: “Exposing tomato plants to a light spectrum dominated by blue wavelengths will result in faster growth rates than when exposed to a light spectrum dominated by red wavelengths.”

This good thesis statement is testable because one can set up an experiment with tomato plants, expose them to different light spectra, and then measure and compare their growth rates to validate or refute the claim.

100 Testing Statement Examples

Size: 237 KB

1. Climate Science : Increased carbon dioxide levels directly correlate with rising global temperatures.

2. Nutrition : Consuming probiotics daily reduces digestive problems in adults over 50.

3. Psychology : Exposure to violent video games increases aggressive behavior in teenagers.

4. Marine Biology : Coral reefs exposed to warmer water temperatures are more susceptible to bleaching events.

5. Astrophysics : Stars of greater mass have shorter lifespans than their lower mass counterparts.

6. Sociology : Students attending single-gender schools perform better academically than those in co-ed schools.

7. Pharmacology : Drug X reduces the symptoms of depression more effectively than Drug Y.

8. Sports Science : Athletes consuming isotonic drinks during workouts experience less muscle fatigue than those drinking water.

9. Economics : Increasing minimum wage by 10% leads to a 2% rise in unemployment.

10. Environmental Science : Deforestation rates are directly proportional to the increase in global carbon emissions.

11. Digital Media : Adults who spend more than 3 hours on social media daily report higher levels of anxiety.

12. Architecture : Urban green spaces reduce surrounding temperatures by at least 2°C.

13. Neurology : Meditation practices increase gray matter concentration in the brain.

14. Agriculture : Genetically modified crops yield 20% more produce than traditional crops.

15. Zoology : Migratory patterns of Monarch butterflies are influenced by global warming.

16. Chemical Engineering : Nanomaterial X is more efficient in cleaning oil spills than Nanomaterial Y.

17. Linguistics : Bilingual children develop cognitive skills faster than monolingual peers.

18. Archeology : Ancient settlements near rivers were 50% larger than those inland.

19. Geology : Areas with higher underground water tables experience fewer earthquakes.

20. Genetics : Gene X is responsible for hair color variation in mammals.

21. Political Science : Nations with proportional representation have higher voter turnout than those with majoritarian systems.

22. Biotechnology : Enzyme Z speeds up the waste decomposition process.

23. Immunology : Vaccine A provides a 95% immunity rate against Disease B.

24. Dermatology : Exposure to UV rays increases skin aging by 40%.

25. Robotics : Robots equipped with Sensor Y detect obstacles 30% faster.

26. Literature : Reading fiction improves empathy in individuals more than reading non-fiction.

27. Quantum Physics : Particle X exhibits wave-particle duality under Condition Y.

28. Geography : Urban areas experience a 10% higher heat index due to the heat island effect.

29. Anthropology : Hunter-gatherer societies had a more varied diet than early agrarian societies.

30. Pediatric Medicine : Children vaccinated with Vaccine C have a 70% lower chance of contracting Disease D.

31. Forestry : Regions with controlled forest fires exhibit a 20% increase in biodiversity.

32. Philosophy : Students exposed to ethical philosophy courses display higher moral reasoning.

33. Astronomy : Planetary bodies in Zone Z have a higher likelihood of supporting life.

34. Musicology : Classical music enhances cognitive performance more than other genres.

35. Ornithology : Birds in urban areas adapt their songs to overcome noise pollution.

36. Culinary Science : Cooking method X retains more nutrients in vegetables than method Y.

37. Meteorology : Regions with rapid urbanization experience unpredictable rainfall patterns.

38. History : Societies with written scripts advanced faster in trade than those without.

39. Ethnology : Indigenous tribes with oral traditions have a richer folklore than those relying on written records.

40. Oceanography : Deep-sea vents are hotspots for undiscovered species.

41. Mathematics : Teaching method X enhances problem-solving skills in students more effectively.

42. Art History : Renaissance artists exposed to human anatomy produced more realistic artworks.

43. Virology : Virus V transmits faster in colder climates.

44. Aeronautics : Planes using Material M are 20% more fuel-efficient.

45. Paleontology : Dinosaurs from Era E had a higher diversity in diet.

46. Entomology : Insects exposed to Pesticide P show increased resistance after 5 generations.

47. Environmental Health : Cities with green transportation have 30% fewer respiratory illness cases.

48. Criminology : Areas with community policing report a 15% decrease in violent crimes.

49. Botany : Plants in high CO2 environments grow 25% faster.

50. Veterinary Medicine : Dogs fed Diet D have shinier coats than those on Diet E.

51. Mycology : Fungi in humid conditions produce 30% more spores than those in arid conditions.

52. Cinematography : Movies with diverse casts garner 20% more global box office revenue.

53. Hydrology : Regions with consistent yearly rainfall have 10% denser vegetation cover.

54. Cosmetology : Products with Ingredient F reduce skin wrinkles more effectively than those with Ingredient G.

55. Endocrinology : Individuals with higher levels of Hormone H tend to have faster metabolism rates.

56. Demography : Urban areas with green spaces have a 15% higher life expectancy rate.

57. Acoustics : Materials using Tech I have a noise reduction rate of 50% in urban environments.

58. Gastronomy : Foods cooked using Technique J retain 90% of their original flavor profile.

59. Hematology : Patients treated with Drug K show a 40% decrease in blood clotting issues.

60. Theology : Societies with polytheistic beliefs have a more diverse set of rituals than monotheistic ones.

61. Optometry : Individuals exposed to Screen L for over 5 hours daily are 25% more likely to develop vision problems.

62. Microbiology : Bacteria M shows a 60% higher resistance to Antibiotic N.

63. Seismology : Areas with deep underground mining activities experience a 20% increase in minor seismic activities.

64. Paleobotany : Plant fossils from Period O indicate a warmer climate than previously thought.

65. Radiology : Equipment using Tech P provides 30% clearer imaging in soft tissues.

66. Choreography : Dance routines incorporating Technique Q improve muscular coordination by 40%.

67. Ornithology : Birds migrating through Route R have a 15% higher survival rate.

68. Astrobiology : Planets in Zone S have conditions 10% more similar to Earth’s primordial state.

69. Gerontology : Elderly individuals engaging in Activity T have a 20% slower cognitive decline.

70. Pedagogy : Students taught using Method U show a 30% improvement in retention rates.

71. Rheumatology : Patients treated with Drug V experience a 50% reduction in joint pain.

72. Ichthyology : Fish in Region W exhibit a 20% more diverse set of behaviors.

73. Mythology : Civilizations with oceanic myths have a 15% higher rate of seafaring activities.

74. Urology : Consuming Substance X leads to a 40% decrease in kidney stone formation.

75. Podiatry : Footwear with Design Y reduces foot fatigue by 25%.

76. Toxicology : Animals exposed to Chemical Z show a 30% increase in liver complications.

77. Ethnomusicology : Communities with traditional drumming rituals have a 20% richer rhythmic pattern.

78. Egyptology : Pharaohs in Dynasty A had a life expectancy 10% higher than those in Dynasty B.

79. Dermatology : Skin exposed to Treatment C shows a 70% reduction in acne breakouts.

80. Lexicography : Languages with phonetic scripts have a 20% faster literacy rate among learners.

81. Zoopharmacognosy : Animals in Region D tend to select Medicinal Plant E 30% more frequently when experiencing digestive issues.

82. Meteorology : Places with increasing urban surfaces witness a 25% increase in lightning activity.

83. Epistemology : Societies valuing experiential knowledge record 40% more oral histories.

84. Nephrology : Individuals consuming Water Source F show a 20% lower risk of kidney-related diseases.

85. Graphology : People with angular handwriting exhibit a 15% higher tendency towards analytical thinking.

86. Mammalogy : Mammals in Altitude G have a 30% denser fur compared to those at sea level.

87. Graph theory : Networks designed using Algorithm H are 50% more efficient in data transfer.

88. Pomology : Trees treated with Fertilizer I produce fruits that are 20% larger in size.

89. Photobiology : Plants exposed to Light J for 6 hours daily have a 25% increase in photosynthetic activity.

90. Ethology : Species K, when isolated, develop a 40% more diverse set of vocal calls.

91. Cryptography : Systems using Encryption L are 30% harder to breach than conventional methods.

92. Phenomenology : Communities that engage in Reflective Practice M have a 20% richer shared cultural experience.

93. Climatology : Regions under Ozone Layer N witness a 15% faster rate of skin-related ailments.

94. Bibliology : Manuscripts preserved using Technique O retain 90% of their original color over centuries.

95. Epigraphy : Stone inscriptions in Region P show a 10% higher consistency in language structure.

96. Tribology : Materials coated with Substance Q have a 50% reduction in wear and tear.

97. Phonology : Languages with Tonal Structure R have a 20% more complex set of vowel sounds.

98. Enology : Grapes cultivated in Region S produce wines with a 15% richer aromatic profile.

99. Aerobiology : Areas with Air Stream T see a 30% increase in pollen dispersion.

100. Cytology : Cells treated with Compound U show a 25% faster regeneration rate.

Non Testable Hypothesis Statement Examples

Non-testable hypothesis are statements that cannot be empirically measured, confirmed, or refuted with experiments. They often reflect subjective, philosophical, or theoretical positions and can be based on personal beliefs or assumptions. In addition, you should review our  null hypothesis in statistics .

1. Spirituality : The soul continues its journey after physical death.

2. Morality : Acts of kindness come from inherent human goodness.

3. Philosophy : The meaning of life is subjective and differs for each individual.

4. Aesthetics : Classical music is superior to pop music.

5. Perception : Dreams are gateways to another dimension.

6. Astrology : Leo signs are born leaders.

7. Literature : Shakespeare’s works have a timeless essence that speaks to every generation.

8. Belief : Fate and destiny control all life events.

9. Theology : Angels watch over humans and protect them from harm.

10. Art : The Mona Lisa captures the essence of mysterious beauty.

Testable Hypothesis Statement Examples in Psychology

Hypothesis psychology often revolve around understanding behavior, emotions, cognitive processes, and the effects of various factors on mental health and human interactions.

1. Childhood Development : Children exposed to bilingual environments before age 5 show enhanced cognitive flexibility.

2. Cognitive : Memory recall is 20% better with visual aids compared to auditory cues.

3. Behavior : Prolonged screen time causes a 15% increase in anxiety levels among teenagers.

4. Emotional Health : Daily meditation reduces stress markers by 25%. 5. Learning Styles : Kinesthetic learners retain 30% more information through hands-on activities.

6. Motivation : Employees with regular feedback are 40% more productive.

7. Social Psychology : Group discussions increase problem-solving efficiency by 20%.

8. Therapy : CBT techniques reduce depression symptoms in 70% of patients.

9. Perception : Exposure to color blue increases calmness levels by 10%.

10. Personality : Extroverts exhibit a 15% higher dopamine response in social situations.

Test Hypothesis Statement Examples in Biology

Biological simple hypothesis dive into the intricacies of life, organisms, and the environmental interactions affecting them, often leaning on empirical evidence and experimentation.

1. Genetics : Genotype AA increases resistance to Disease B by 50%.

2. Ecology : Forest regions with diversified flora show 20% higher insect species richness.

3. Evolution : Species C exhibits a 30% faster mutation rate under environmental stress.

4. Physiology : Plants in high CO2 environments display a 40% increase in growth rate.

5. Biochemistry : Enzyme D catalyzes Reaction E 25% more efficiently at pH 6.

6. Microbiology : Bacterium F grows 15% faster in aerobic conditions.

7. Zoology : Mammal G hibernates for 20% longer when food sources are scarce.

8. Marine Biology : Coral reefs in Area H recover 30% slower with rising sea temperatures.

9. Botany : Plant species I exhibits a 10% higher pollination rate in sunlight.

10. Cellular Biology : Cells exposed to Substance J show a 50% increase in metabolic activity.

Testing Hypothesis Statement Examples in Medicine

In the medical realm, hypothesis concern the effects of treatments, understanding diseases, patient care, and other health-related phenomena.

1. Pharmacology : Drug K reduces pain symptoms in 60% of patients with Condition L.

2. Neurology : Meditation improves neural connectivity in 40% of practitioners.

3. Oncology : Treatment M increases the survival rate of cancer patients by 20%.

4. Cardiology : Diet N decreases the risk of heart diseases by 25%.

5. Endocrinology : Hormone O levels correlate with a 15% rise in mood disorders.

6. Immunology : Vaccine P offers 90% protection against Virus Q.

7. Nutrition : Diet R rich in Omega-3s reduces inflammation in 70% of individuals.

8. Surgery : Procedure S improves mobility in 80% of joint replacement patients.

9. Pediatrics : Early exposure to Allergen T decreases allergy risk by 30%.

10. Dermatology : Cream U reduces skin blemishes in 50% of users within one month.

Testing Hypothesis Statement Examples in Research

Research hypothesis span a wide range of disciplines and involve a clear, measurable statement that can be empirically tested using rigorous methods.

1. Social Sciences : Socio-economic factors account for a 40% variance in academic achievements.

2. Environmental Research : City V’s waste reduction program will decrease landfill contributions by 30%.

3. Economic Research : Implementing Policy W increases local businesses’ revenue by 20%.

4. Educational Research : Incorporating Technology X in classrooms boosts student engagement by 25%.

5. Agricultural Research : Crop Y, when genetically modified, shows a 50% increase in drought resistance.

6. Space Research : Celestial Body Z has conditions 15% similar to Earth, supporting potential life.

7. Chemical Research : Compound A reacts with Compound B producing 30% more energy.

8. Political Science : Implementing Voting System C will increase voter turnout by 20%.

9. Climate Research : A 10% rise in greenhouse gas concentrations correlates with a 1°C increase in global temperatures.

10. Linguistic Research : Bilingual individuals learn a third language 25% faster.

How do you write a Testing Hypothesis? – Step by Step Guide

A testing scientific hypothesis is a foundational concept in the scientific method, establishing an initial premise to be tested through research and experimentation. Constructing a clear, concise, and testable hypothesis is vital for reliable and valid experimental research. Here’s how to craft one:

1. Identify the Problem

Before you can form a hypothesis, you need to identify a specific problem or question that you want to explore. This often arises from prior observations, existing literature, or curiosity.

2. Conduct Preliminary Research

Survey existing literature on your topic. This will give you a better understanding of the subject and might shed light on areas that haven’t been studied extensively.

3. Define the Variables

Every hypothesis has two key components:

• The independent variable (what you change).
• The dependent variable (what you observe or measure).

For instance, in the hypothesis, “If I water plants with a liquid nutrient, they will grow faster”, the liquid nutrient is the independent variable, and the growth rate of the plants is the dependent variable.

4. Formulate Your Hypothesis

Begin with an “If-Then” statement. “If [I do this], then [this] will happen.” Ensure it’s clear and concise.

5. Ensure Testability

Your hypothesis must be testable through experiments, observations, or other empirical means. It should also be falsifiable, meaning there must be a potential outcome that could demonstrate the hypothesis is incorrect.

6. State It Simply

A good hypothesis is straightforward and simple. Avoid jargon and complex language.

7. Be Specific

A vague hypothesis is difficult to test. Ensure that terms are clearly defined and concepts are specific.

8. Seek Feedback

Before proceeding, share your hypothesis with colleagues, mentors, or peers to gain feedback. They might see aspects you’ve missed.

9. Revise if Necessary

Based on feedback or further reflection, refine your hypothesis to make it as strong as possible.

10. Test the Hypothesis

Design and conduct experiments to evaluate the hypothesis. Remember, the goal is not to “prove” but to “test” it.

Tips for Writing a Testing Thesis Statement

A testing thesis statement provides the foundation for research papers, setting the tone and direction of the study. Here’s how to ensure it’s robust and compelling:

1. Clarify Your Research Question

A clear research question is the foundation of a solid thesis statement. It defines what you wish to learn or clarify.

2. Position It Early

Typically, the testing thesis statement should appear early in your paper, often at the end of the introductory paragraph.

3. Stay Focused

Your thesis statement should be specific and reflect exactly what you will cover in your paper. Avoid vague terms and broad topics.

4. Ensure it’s Arguable

A good thesis statement presents a claim or an interpretation that others might challenge. It should not be a mere statement of fact.

5. Keep It Concise

Aim for one to two sentences. If it’s getting longer, see if you can pare it down or refine your focus.

6. Avoid Formulaic Phrases

Phrases like “This essay will…” or “The purpose of this paper is…” can weaken your thesis. Instead, make a definitive statement about your topic.

7. Revisit and Revise

As you conduct your research, be prepared to adjust or tweak your thesis statement. Research is a process of discovery, and you may find your perspective shifting.

8. Seek Clarity

Every word in your thesis statement should be necessary. If you can remove a word and the statement remains clear, do so.

9. Avoid Overly Technical Language

Unless you’re writing for a specialist audience, avoid jargon or overly technical language. Your thesis should be understandable to a broad audience.

10. Stand by Your Thesis

It’s a commitment to your reader about the content, purpose, and organization of your paper. Ensure every part of your paper relates back to and supports your thesis statement.

Text prompt

• Instructive
• Professional

10 Examples of Public speaking

20 Examples of Gas lighting

Calcworkshop

Hypothesis Testing w/ 21 Step-by-Step Examples!

// Last Updated: October 9, 2020 - Watch Video //

In statistical testing, also referred to as hypothesis testing, our goal is to show the credibility of a claim regarding the population.

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

What Is Hypothesis Testing

Now it would be unreasonable to assume that we can test the entire population to determine the feasibility of every claim one might have.

Thus, we need a way to conclude an assumption is true or false by taking an appropriate sample and calculating a relevant statistic.

And knowing that we must expect that there will be some variation between the sample statistic that is calculated and the true population parameter, leads us to the understanding of statistical inferences (hypotheses).

Hypothesis Testing Steps

First, we must identify the parameter of interest.

Remember that a parameter always points to the population so that it will be either a population mean, population proportion, population slope, or some other population parameter.

Types of Hypothesis Tests

Then we will write a declaration of our significance test, which will include a null hypothesis statement and an alternative hypothesis.

The null hypothesis is the expected value of the population parameter, similar to the status quo, whereas the alternative hypothesis is a statement of negation of the null hypothesis as discussed by Penn State .

Next, we will calculate the desired test statistic from our random sample. This test statistic is a numerical quantity that measures the difference between the observed value and the expected value, divided by the standard error, which is the sample standard deviation.

Then we will compare this test statistic with a specified level of significance (alpha), just like we did with confidence intervals.

If the probability of yielding the sample statistic is as extreme or more extreme is smaller than our significance level, then we declare the sample statistic to be significant and reject the null hypothesis in favor of the alternative. In other words, if the probability is inside our shaded critical region then it is considered more extreme; thus, rejecting the hypothesis. But if it is outside the critical region, we will fail to reject our claim in favor of the alternative.

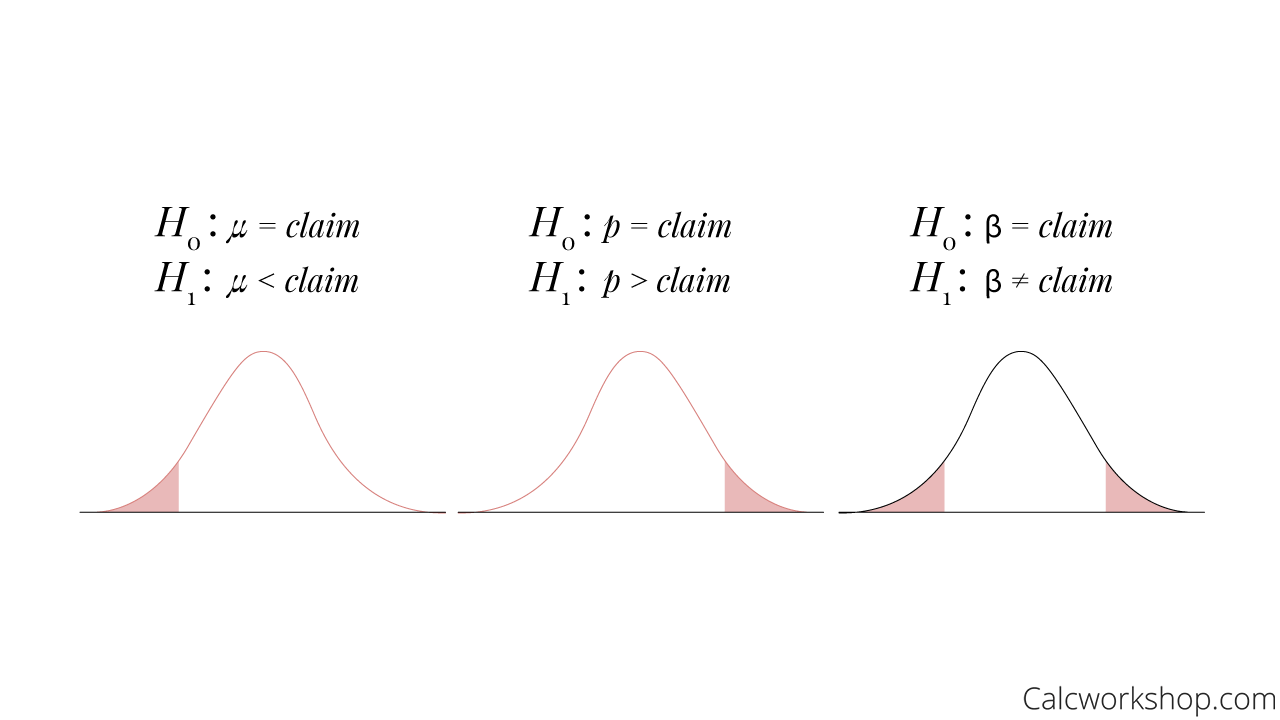
Null and Alternative Hypothesis

Additionally, we will also learn how to determine whether our study calls for a one or two-tailed test.

Type 1 And Type 2 Errors

Now, with all inferences and tests of significance, there is always room for error. A Type I error occurs if we reject the null hypothesis, when in actuality, the null hypothesis is true. Similarly, if we fail to reject the null hypothesis when, in reality, the null hypothesis is false, this is considered a Type II error .

Type 1 Vs. Type 2 Error

Imagine you are in a court of law, where a defendant is presumed innocent until proven guilty. What possible errors could a jury make regarding the outcome of the trial?

First, let’s state the following:

• The Null Hypothesis: The defendant is innocent.
• The Alternative Hypothesis: the defendant is guilty.

Now, a Type I Error would happen if the jury rejects the null hypothesis as false when, in reality, the null hypothesis is true. In other words, the jury finds the defendant guilty of a crime they didn’t commit.

And a Type II Error is when a jury accepts the null hypothesis as true when, in reality, the null hypothesis is false. Meaning, the defendant is found innocent of a crime they did commit.

Let’s look at an example where we put all of these ideas together.

Worked Example

Imagine we have a textile manufacturer investigating a new yarn, which claims it has a thread elongation of 12 kilograms with a standard deviation of 0.5 kilograms.

Using a random sample of 4 specimens, the manufacturer wishes to test the claim that the mean thread elongation is less than 12 kilograms.

Write a hypothesis statement for this scenario and using a normal distribution, find the Type 1 error if the sample mean is less than 11.5 kilograms.

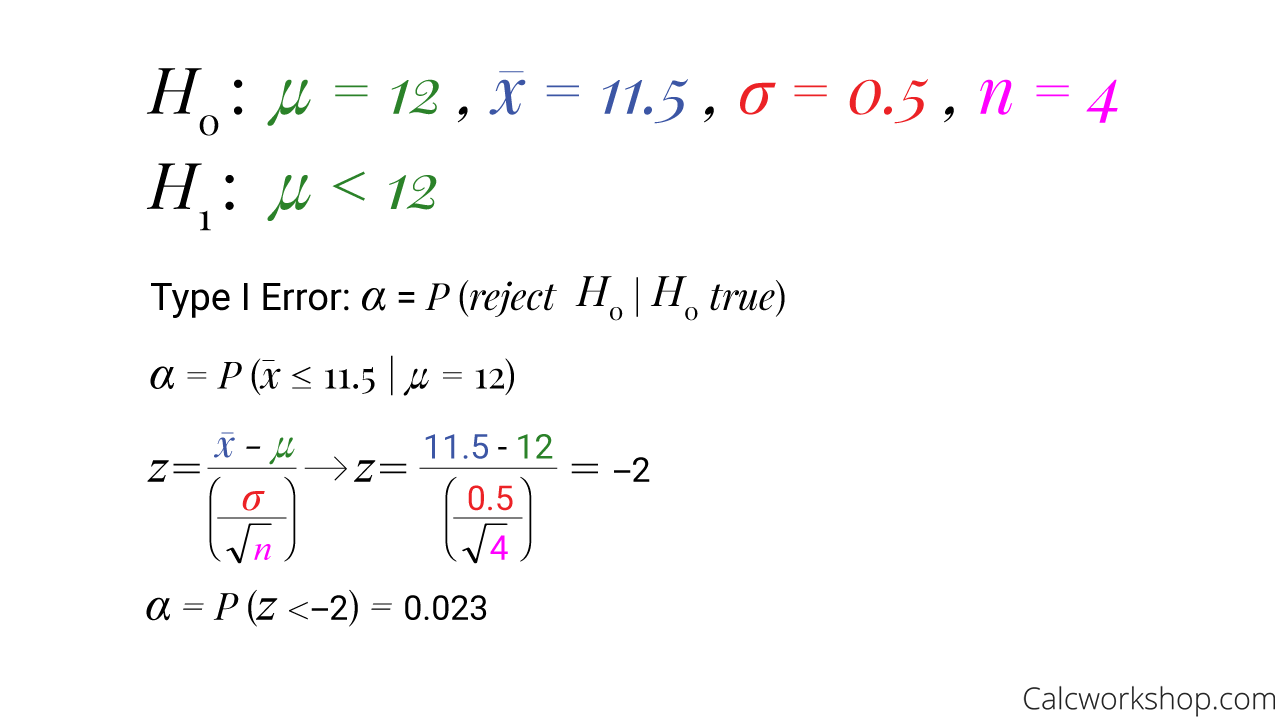
Type 1 Error — Example

As we can see, from the example above, the likelihood of a type I error, where the manufacturer rejects the null hypothesis when the null hypothesis is actually true, is approximately 0.023 or 2.3% likely.

Together, we will look at these two types of error and how they affect decision-making and begin to explore the notion of a probability value and how it helps us determine the validity or falsity of our claim.

Hypothesis Testing – Lesson & Examples (Video)

1 hr 17 min

• Introduction to Video: Statistical Hypotheses
• 00:00:38 – Overview of Hypothesis Testing and determining a correctly stated hypothesis testing problem (Examples #1-7)
• Exclusive Content for Members Only
• 00:14:34 – State the Null Hypothesis and the Alternative Hypothesis for each scenario (Examples #8-12)
• 00:25:46 – Hypothesis Testing Steps and Overview of Type I and Type II errors (Examples #13-14)
• 00:40:32 – Describe a Type 1 and Type 2 error (Examples #15-16)
• 00:46:32 – Overview of p-value and Tails of the Hypothesis Test
• 00:55:55 – Find the probability of a Type I and Type II error (Example #17)
• 01:06:08 – Identify null hypothesis, alternative hypothesis, and state whether the scenario is a one-tail or two-tailed test (Examples #18-21)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.