data structure problem solving types

EnjoyMathematics

Problem-Solving Approaches in Data Structures and Algorithms

This blog highlights some popular problem-solving strategies for solving problems in DSA. Learning to apply these strategies could be one of the best milestones for the learners in mastering data structure and algorithms.

An Incremental approach using Single and Nested loops

One of the simple ideas of our daily problem-solving activities is that we build the partial solution step by step using a loop. There is a different variation to it:

• Input-centric strategy: At each iteration step, we process one input and build the partial solution.
• Output-centric strategy: At each iteration step, we add one output to the solution and build the partial solution.
• Iterative improvement strategy: Here, we start with some easily available approximations of a solution and continuously improve upon it to reach the final solution.

Here are some approaches based on loop: Using a single loop and variables, Using nested loops and variables, Incrementing the loop by a constant (more than 1), Using the loop twice (Double traversal), Using a single loop and prefix array (or extra memory), etc.

Example problems:   Insertion Sort ,  Finding max and min in an array ,  Valid mountain array ,  Find equilibrium index of an array ,  Dutch national flag problem ,  Sort an array in a waveform .

Decrease and Conquer Approach

This strategy is based on finding the solution to a given problem via its one sub-problem solution. Such an approach leads naturally to a recursive algorithm, which reduces the problem to a sequence of smaller input sizes. Until it becomes small enough to be solved, i.e., it reaches the recursion’s base case.

Example problems:   Euclid algorithm of finding GCD ,  Binary Search ,  Josephus problem

Problem-solving using Binary Search

When an array has some order property similar to the sorted array, we can use the binary search idea to solve several searching problems efficiently in O(logn) time complexity. For doing this, we need to modify the standard binary search algorithm based on the conditions given in the problem. The core idea is simple: calculate the mid-index and iterate over the left or right half of the array.

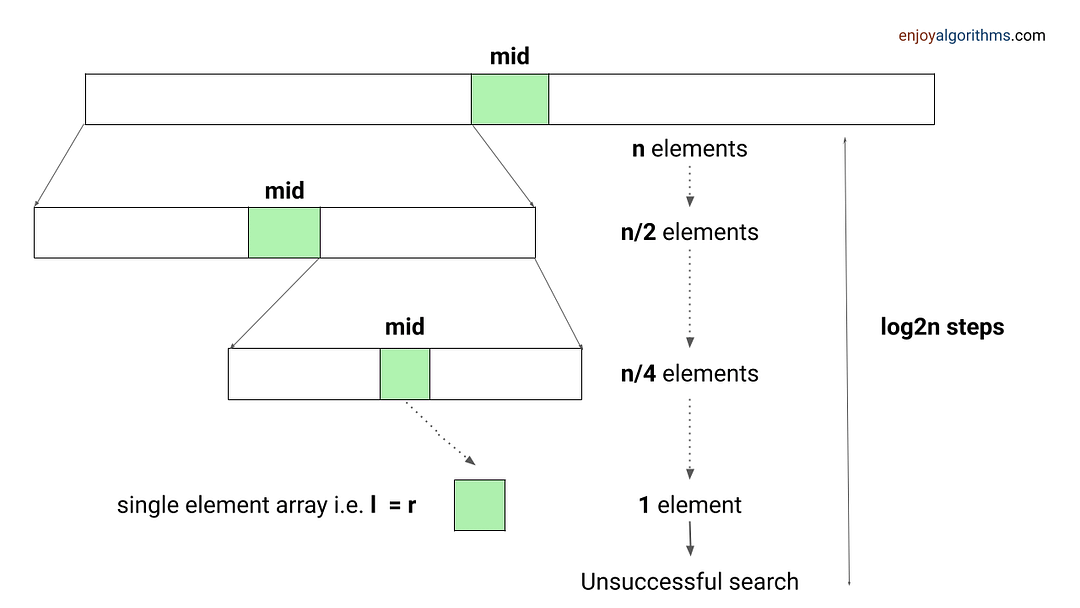
Example problems: Find Peak Element , Search a sorted 2D matrix , Find the square root of an integer , Search in Rotated Sorted Array

Divide and Conquer Approach

This strategy is about dividing a problem into  more than one subproblems,  solving each of them, and then, if necessary, combining their solutions to get a solution to the original problem. We solve many fundamental problems efficiently in computer science by using this strategy.

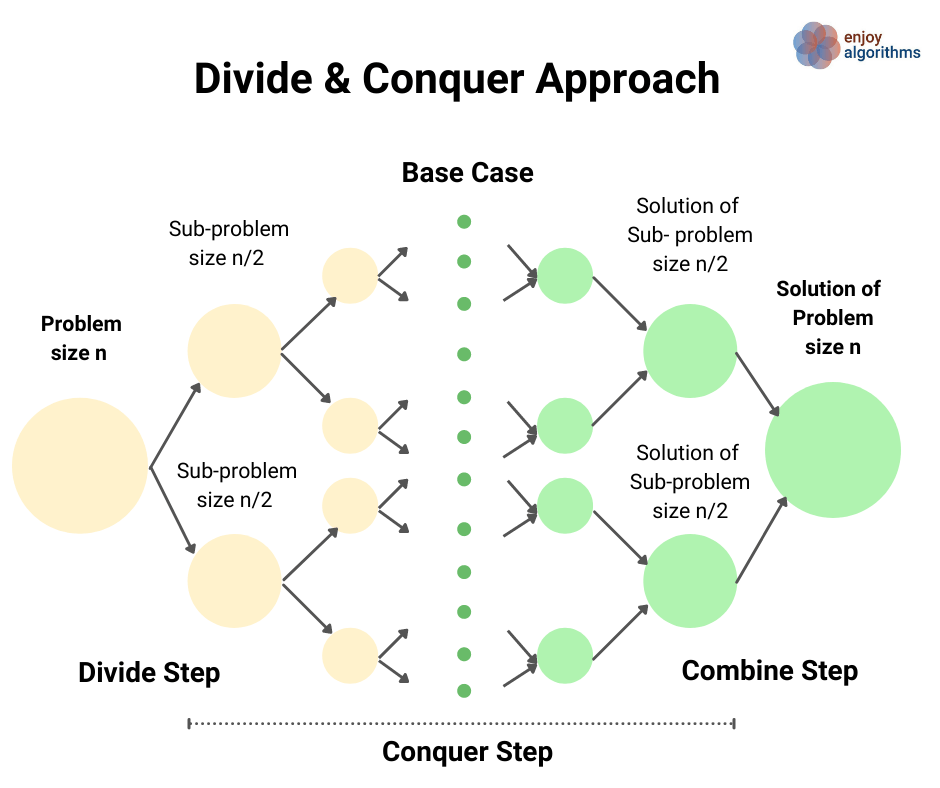
Example problems:   Merge Sort ,  Quick Sort ,  Median of two sorted arrays

Two Pointers Approach

The two-pointer approach helps us optimize time and space complexity in the case of many searching problems on arrays and linked lists. Here pointers can be pairs of array indices or pointer references to an object. This approach aims to simultaneously iterate over two different input parts to perform fewer operations. There are three variations of this approach:

Pointers are moving in the same direction with the same pace:   Merging two sorted arrays or linked lists, Finding the intersection of two arrays or linked lists , Checking an array is a subset of another array , etc.

Pointers are moving in the same direction at a different pace (Fast and slow pointers):   Partition process in the quick sort , Remove duplicates from the sorted array , Find the middle node in a linked list , Detect loop in a linked list , Move all zeroes to the end , Remove nth node from list end , etc.

Pointers are moving in the opposite direction:  Reversing an array, Check pair sum in an array , Finding triplet with zero-sum , Rainwater trapping problem , Container with most water , etc.

Sliding Window Approach

A sliding window concept is commonly used in solving array/string problems. Here, the window is a contiguous sequence of elements defined by the start and ends indices. We perform some operations on elements within the window and “slide” it in a forward direction by incrementing the left or right end.

This approach can be effective whenever the problem consists of tasks that must be performed on a contiguous block of a fixed or variable size. This could help us improve time complexity in so many problems by converting the nested loop solution into a single loop solution.

Example problems: Longest substring without repeating characters , Count distinct elements in every window , Max continuous series of 1s , Find max consecutive 1's in an array , etc.

Transform and Conquer Approach

This approach is based on transforming a coding problem into another coding problem with some particular property that makes the problem easier to solve. In other words, here we solve the problem is solved in two stages:

• Transformation stage: We transform the original problem into another easier problem to solve.
• Conquering stage: Now, we solve the transformed problem.

Example problems: Pre-sorting based algorithms (Finding the closest pair of points, checking whether all the elements in a given array are distinct, etc.)

Problem-solving using BFS and DFS Traversal

Most tree and graph problems can be solved using DFS and BFS traversal. If the problem is to search for something closer to the root (or source node), we can prefer BFS, and if we need to search for something in-depth, we can choose DFS.

Sometimes, we can use both BFS and DFS traversals when node order is not required. But in some cases, such things are not possible. We need to identify the use case of both traversals to solve the problems efficiently. For example, in binary tree problems:

• We use preorder traversal in a situation when we need to explore all the tree nodes before inspecting any leaves.
• Inorder traversal of BST generates the node's data in increasing order. So we can use inorder to solve several BST problems.
• We can use postorder traversal when we need to explore all the leaf nodes before inspecting any internal nodes.
• Sometimes, we need some specific information about some level. In this situation, BFS traversal helps us to find the output easily.

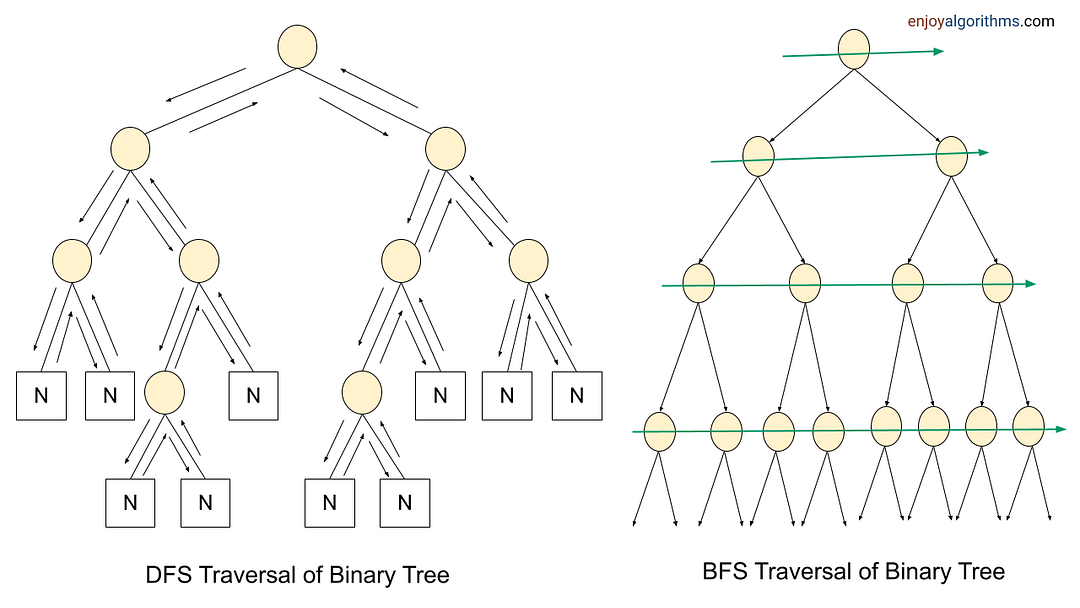
To solve tree and graph problems, sometimes we pass extra variables or pointers to the function parameters, use helper functions, use parent pointers, store some additional data inside the node, and use data structures like the stack, queue, and priority queue, etc.

Example problems: Find min depth of a binary tree , Merge two binary trees , Find the height of a binary tree , Find the absolute minimum difference in a BST , The kth largest element in a BST , Course scheduling problem , bipartite graph , Find the left view of a binary tree , etc.

Problem-solving using the Data Structures

The data structure is one of the powerful tools of problem-solving in algorithms. It helps us perform some of the critical operations efficiently and improves the time complexity of the solution. Here are some of the key insights:

• Many coding problems require an effcient way to perform the search, insert and delete operations. We can perform all these operations using the hash table in O(1) time average. It's a kind of time-memory tradeoff, where we use extra space to store elements in the hash table to improve performance.
• Sometimes we need to store data in the stack (LIFO order) or queue (FIFO order) to solve several coding problems. 
• Suppose there is a requirement to continuously insert or remove maximum or minimum element (Or element with min or max priority). In that case, we can use a heap (or priority queue) to solve the problem efficiently.
• Sometimes, we store data in Trie, AVL Tree, Segment Tree, etc., to perform some critical operations efficiently. 

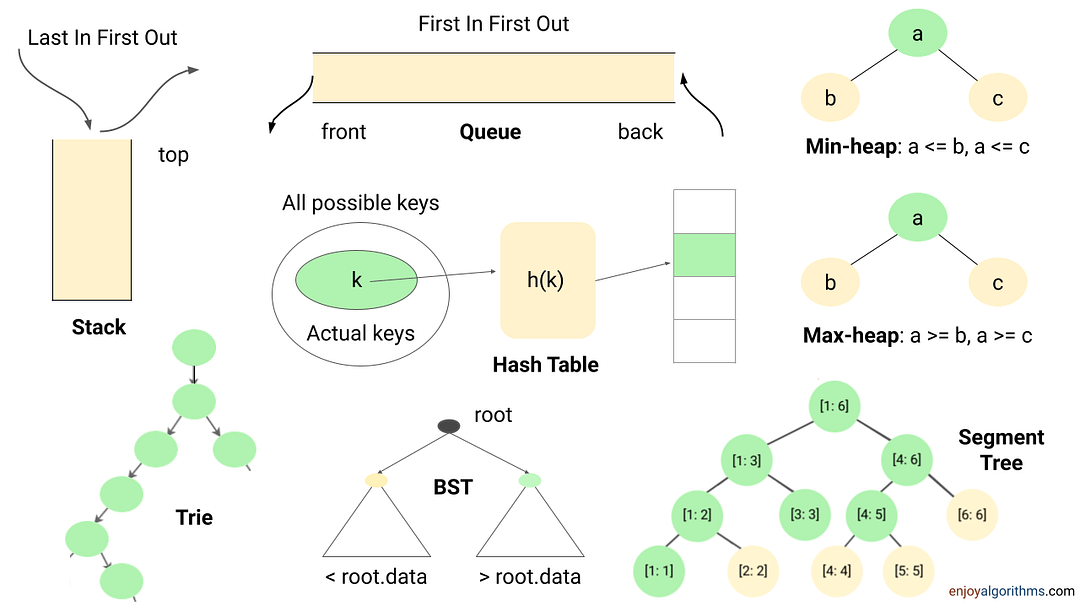
Example problems: Next greater element , Valid Parentheses , Largest rectangle in a histogram , Sliding window maximum , kth smallest element in an array , Top k frequent elements , Longest common prefix , Range sum query , Longest consecutive sequence , Check equal array , LFU cache , LRU cache , Counting sort

Dynamic Programming

Dynamic programming is one of the most popular techniques for solving problems with overlapping or repeated subproblems. Here rather than solving overlapping subproblems repeatedly, we solve each smaller subproblems only once and store the results in memory. We can solve a lot of optimization and counting problems using the idea of dynamic programming.

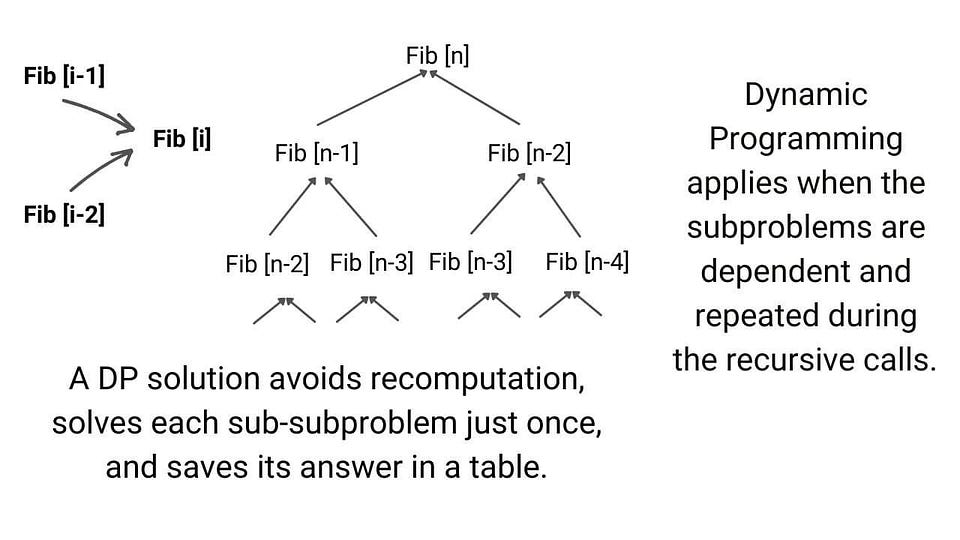
Example problems: Finding nth Fibonacci,  Longest Common Subsequence ,  Climbing Stairs Problem ,  Maximum Subarray Sum ,  Minimum number of Jumps to reach End ,  Minimum Coin Change

Greedy Approach

This solves an optimization problem by expanding a partially constructed solution until a complete solution is reached. We take a greedy choice at each step and add it to the partially constructed solution. This idea produces the optimal global solution without violating the problem’s constraints.

• The greedy choice is the best alternative available at each step is made in the hope that a sequence of locally optimal choices will yield a (globally) optimal solution to the entire problem.
• This approach works in some cases but fails in others. Usually, it is not difficult to design a greedy algorithm itself, but a more difficult task is to prove that it produces an optimal solution.

Example problems: Fractional Knapsack, Dijkstra algorithm, The activity selection problem

Exhaustive Search

This strategy explores all possibilities of solutions until a solution to the problem is found. Therefore, problems are rarely offered to a person to solve the problem using this strategy.

The most important limitation of exhaustive search is its inefficiency. As a rule, the number of solution candidates that need to be processed grows at least exponentially with the problem size, making the approach inappropriate not only for a human but often for a computer as well.

But in some situations, there is a need to explore all possible solution spaces in a coding problem. For example: Find all permutations of a string , Print all subsets , etc.

Backtracking

Backtracking is an improvement over the approach of exhaustive search. It is a method for generating a solution by avoiding unnecessary possibilities of the solutions! The main idea is to build a solution one piece at a time and evaluate each partial solution as follows:

• If a partial solution can be developed further without violating the problem’s constraints, it is done by taking the first remaining valid option at the next stage. ( Think! )
• Suppose there is no valid option at the next stage, i.e., If there is a violation of the problem constraint, the algorithm backtracks to replace the partial solution’s previous stage with the following option for that stage. ( Think! )

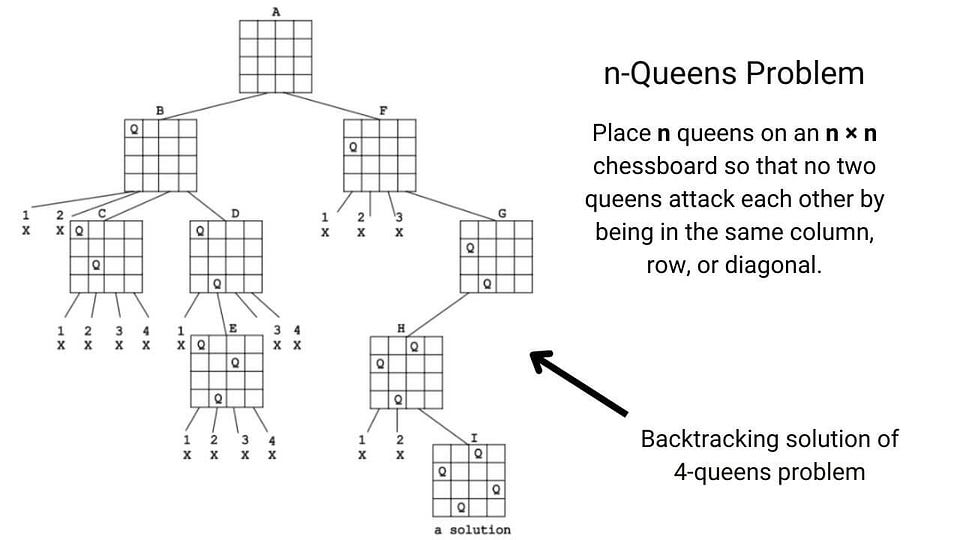
In simple words, backtracking involves undoing several wrong choices — the smaller this number, the faster the algorithm finds a solution. In the worst-case scenario, a backtracking algorithm may end up generating all the solutions as an exhaustive search, but this rarely happens!

Example problems: N-queen problem , Find all k combinations , Combination sum , Sudoku solver , etc.

Problem-solving using Bit manipulation and Numbers theory

Some of the coding problems are, by default, mathematical, but sometimes we need to identify the hidden mathematical properties inside the problem. So the idea of number theory and bit manipulation is helpful in so many cases.

Sometimes understanding the bit pattern of the input and processing data at the bit level help us design an efficient solution. The best part is that the computer performs each bit-wise operation in constant time. Even sometimes, bit manipulation can reduce the requirement of extra loops and improve the performance by a considerable margin.

Example problems: Reverse bits , Add binary string , Check the power of two , Find the missing number , etc.

Hope you enjoyed the blog. Later we will write a separate blog on each problem-solving approach. Enjoy learning, Enjoy algorithms!

Share Your Insights

Don’t fill this out if you’re human:

More from EnjoyAlgorithms

Self-paced courses and blogs, coding interview, machine learning, system design, oop concepts, our newsletter.

Subscribe to get well designed content on data structure and algorithms, machine learning, system design, object orientd programming and math.

©2023 Code Algorithms Pvt. Ltd.

All rights reserved.

• DSA Tutorial
• Data Structures
• Linked List
• Dynamic Programming
• Binary Tree
• Binary Search Tree
• Divide & Conquer
• Mathematical
• Backtracking
• Branch and Bound
• Pattern Searching

Data Structures & Algorithms Guide for Developers

As a developer, understanding data structures and algorithms is crucial for writing efficient and scalable code. Here is a comprehensive guide to help you learn and master these fundamental concepts:

Introduction to Algorithms and Data Structures (DSA) :

• Data Structures and Algorithms are foundational concepts in computer science that play a crucial role in solving computational problems efficiently.
• Data structures are organized and stored in formats to enable efficient data manipulation and retrieval. They provide a way to organize and store data so that operations can be performed efficiently. Some of the common data structures that every developer should know are Arrays, Linked List, Stack, Queue, Trees, Graphs, etc.
• Algorithms are step-by-step procedures or formulas for solving specific problems. They are a sequence of well-defined, unambiguous instructions designed to perform a specific task or solve a particular problem. Some of the common algorithms that every developer should know are Searching Algorithms, Sorting Algorithms, Graph Algorithms, Dynamic Programming, Divide and Conquer, etc.

Data Structure & Algorithms Guide for Developers

• Introduction to Algorithms and Data Structures (DSA):
• Linked Lists
• Hash Tables
• Sorting Algorithms
• Searching Algorithms
• Bitwise Algorithms
• Greedy Algorithms
• Divide and Conquer
• Algorithm Analysis
• Problem Solving
• Why are Data Structure & Algorithms important in software development
• Additional Resources

Basic Data Structures :

Learn how to create and manipulate arrays, including basic operations like insertion, deletion, and searching

The most basic yet important data structure is the array. It is a linear data structure. An array is a collection of homogeneous data types where the elements are allocated contiguous memory. Because of the contiguous allocation of memory, any element of an array can be accessed in constant time. Each array element has a corresponding index number. 

To learn more about arrays, refer to the article “ Introduction to Arrays “.

Here are some topics about array which you must learn:

• Reverse Array  – Reverse an array means shifting the elements of an array in a reverse manner i.e., the last element becomes the first element, second last element becomes the second element, and so on. 
• Rotation of Array  – Rotation of array means shifting the elements of an array in a circular manner i.e., in the case of right circular shift the last element becomes the first element, and all other element moves one point to the right. 
• Rearranging an array  – Rearrangement of array elements suggests the changing of an initial order of elements following some conditions or operations.
• Range queries in the array  – Often you need to perform operations on a range of elements. These functions are known as range queries.
• Multidimensional array  – These are arrays having more than one dimension. The most used one is the 2-dimensional array, commonly known as a matrix.
• Kadane’s algorithm
• Dutch national flag algorithm

Types of Arrays:

• One-dimensional array (1-D Array): You can imagine a 1d array as a row, where elements are stored one after another.
• Two-dimensional array (2-D Array or Matrix): 2-D Multidimensional arrays can be considered as an array of arrays or as a matrix consisting of rows and columns.
• Three-dimensional array (3-D Array): A 3-D Multidimensional array contains three dimensions, so it can be considered an array of two-dimensional arrays.

Linked Lists:

Understand the concept of linked lists, including singly linked lists, doubly linked lists, and circular linked lists

As the above data structures, the linked list is also a linear data structure. But  Linked List is different from Array  in its configuration. It is not allocated to contiguous memory locations. Instead, each node of the linked list is allocated to some random memory space and the previous node maintains a pointer that points to this node. So no direct memory access of any node is possible and it is also dynamic i.e., the size of the linked list can be adjusted at any time. To learn more about linked lists refer to the article “ Introduction to Linked List “.

The topics which you must want to cover are:

• Singly Linked List  – In this, each node of the linked list points only to its next node.
• Circular Linked List  – This is the type of linked list where the last node points back to the head of the linked list.
• Doubly Linked List  – In this case, each node of the linked list holds two pointers, one point to the next node and the other points to the previous node.

Learn about the stack data structure and their applications

Stack  is a linear data structure which follows a particular order in which the operations are performed. The order may be  LIFO(Last In First Out) or FILO(First In Last Out) .

The reason why Stack is considered a complex data structure is that it uses other data structures for implementation, such as Arrays, Linked lists, etc. based on the characteristics and features of Stack data structure.

Learn about the queue data structure and their applications

Queue is a linear data structure which follows a particular order in which the operations are performed. The order may be FIFO (First In First Out) .

The reason why Queue is considered a complex data structure is that it uses other data structures for implementation, such as Arrays, Linked lists, etc. based on the characteristics and features of Queue data structure.

Understand the concepts of binary trees, binary search trees, AVL trees, and more

After having the basics covered about the  linear data structure , now it is time to take a step forward to learn about the non-linear data structures. The first non-linear data structure you should learn is the tree. 

Tree data structure  is similar to a tree we see in nature but it is upside down. It also has a root and leaves. The root is the first node of the tree and the leaves are the ones at the bottom-most level. The special characteristic of a tree is that there is only one path to go from any of its nodes to any other node.

Based on the maximum number of children of a node of the tree it can be – 

• Binary tree  – This is a special type of tree where each node can have a maximum of 2 children.
• Ternary tree  – This is a special type of tree where each node can have a maximum of 3 children.
• N-ary tree  – In this type of tree, a node can have at most N children.

Based on the configuration of nodes there are also several classifications. Some of them are:

• Complete Binary Tree  – In this type of binary tree all the levels are filled except maybe for the last level. But the last level elements are filled as left as possible.
• Perfect Binary Tree  – A perfect binary tree has all the levels filled
• Binary Search Tree  – A binary search tree is a special type of binary tree where the smaller node is put to the left of a node and a higher value node is put to the right of a node
• Ternary Search Tree  – It is similar to a binary search tree, except for the fact that here one element can have at most 3 children.

Learn about graph representations, graph traversal algorithms (BFS, DFS), and graph algorithms (Dijkstra's, Floyd-Warshall, etc.)

Another important non-linear data structure is the graph. It is similar to the Tree data structure, with the difference that there is no particular root or leaf node, and it can be traversed in any order.

A  Graph  is a non-linear data structure consisting of a finite set of vertices(or nodes) and a set of edges that connect a pair of nodes. 

Each edge shows a connection between a pair of nodes. This data structure helps solve many real-life problems. Based on the orientation of the edges and the nodes there are various types of graphs. 

Here are some must to know concepts of graphs:

• Types of graphs  – There are different types of graphs based on connectivity or weights of nodes.
• Introduction to BFS and DFS  – These are the algorithms for traversing through a graph
• Cycles in a graph  – Cycles are a series of connections following which we will be moving in a loop.
• Topological sorting in the graph
• Minimum Spanning tree in graph

Advanced Data Structures :

Understand the concept of heaps and their applications, such as priority queues

A Heap is a special  Tree-based Data Structure  in which the tree is a complete binary tree.

Types of heaps:

Generally, heaps are of two types.

• Max-Heap :  In this heap, the value of the root node must be the greatest among all its child nodes and the same thing must be done for its left and right sub-tree also.
• Min-Heap :  In this heap, the value of the root node must be the smallest among all its child nodes and the same thing must be done for its left ans right sub-tree also.

Hash Tables:

Learn about hash functions, collision resolution techniques, and applications of hash tables

Hashing  refers to the process of generating a fixed-size output from an input of variable size using the mathematical formulas known as hash functions. This technique determines an index or location for the storage of an item in a data structure.

Understand trie data structures and their applications, such as prefix matching and autocomplete

Trie is a type of k-ary search tree used for storing and searching a specific key from a set. Using Trie, search complexities can be brought to optimal limit (key length). 

A trie (derived from retrieval) is a multiway tree data structure used for storing strings over an alphabet. It is used to store a large amount of strings. The pattern matching can be done efficiently using tries.

• Trie Delete
• Trie data structure
• Displaying content of Trie
• Applications of Trie
• Auto-complete feature using Trie
• Minimum Word Break
• Sorting array of strings (or words) using Trie
• Pattern Searching using a Trie of all Suffixes

Basic Algorithms :

Basic algorithms are the fundamental building blocks of computer science and programming. They are essential for solving problems efficiently and are often used as subroutines in more complex algorithms.

Sorting Algorithms:

Learn about different sorting algorithms like bubble sort, selection sort, insertion sort, merge sort, quicksort, and their time complexity

Sorting Algorithm  is used to rearrange a given array or list elements according to a comparison operator on the elements. The comparison operator is used to decide the new order of element in the respective data structure.

Sorting algorithms are essential in computer science and programming, as they allow us to organize data in a meaningful way. Here's an overview of some common sorting algorithms:

• Description : Bubble sort repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order.
• Time Complexity : O(n^2) in the worst case and O(n) in the best case (when the list is already sorted).
• Description : Selection sort divides the input list into two parts: the sublist of items already sorted and the sublist of items remaining to be sorted. It repeatedly selects the smallest (or largest) element from the unsorted sublist and swaps it with the first element of the unsorted sublist.
• Time Complexity : O(n^2) in all cases (worst, average, and best).
• Description : Insertion sort builds the final sorted array one element at a time by repeatedly inserting the next element into the sorted part of the array.
• Description : Merge sort is a divide-and-conquer algorithm that divides the input list into two halves, sorts each half recursively, and then merges the two sorted halves.
• Time Complexity : O(n log n) in all cases (worst, average, and best).
• Description : Quick sort is a divide-and-conquer algorithm that selects a pivot element and partitions the input list into two sublists: elements less than the pivot and elements greater than the pivot. It then recursively sorts the two sublists.
• Time Complexity : O(n^2) in the worst case and O(n log n) in the average and best cases.
• Description : Heap sort is a comparison-based sorting algorithm that builds a heap from the input list and repeatedly extracts the maximum (or minimum) element from the heap and rebuilds the heap.
• Description : Radix sort is a non-comparison-based sorting algorithm that sorts elements by their individual digits or characters. It sorts the input list by processing the digits or characters from the least significant digit to the most significant digit.
• Time Complexity : O(nk) where n is the number of elements in the input list and k is the number of digits or characters in the largest element.

Searching Algorithms:

Understand linear search, binary search, and their time complexity

Searching algorithms are used to find a particular element or value within a collection of data. Here are two common searching algorithms:

• Description : Linear search, also known as sequential search, checks each element in the list until the desired element is found or the end of the list is reached. It is the simplest and most intuitive searching algorithm.
• Time Complexity : O(n) in the worst case, where n is the number of elements in the list. This is because in the worst case, the algorithm may need to check every element in the list.
• Description : Binary search is a more efficient searching algorithm that works on sorted lists. It repeatedly divides the list in half and checks whether the desired element is in the left or right half. It continues this process until the element is found or the list is empty.
• Time Complexity : O(log n) in the worst case, where n is the number of elements in the list. This is because the algorithm divides the list in half at each step, leading to a logarithmic time complexity.

Comparison:

• Works on both sorted and unsorted lists.
• Time complexity is O(n) in the worst case.
• Simple to implement.
• Works only on sorted lists.
• Time complexity is O(log n) in the worst case.
• More efficient than linear search for large lists.

Understand Recursion, how it works and solve problems about how Recursion can solve complex problems easily

The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. Using a recursive algorithm, certain problems can be solved quite easily. Recursion is one of the most important algorithms which uses the concept of code reusability and repeated usage of the same piece of code. 

A recursive function solves a particular problem by calling itself for smaller subproblems and using those solutions to solve the original subproblem. 

The point which makes Recursion one of the most used algorithms is that it forms the base for many other algorithms such as:

• Tree traversals
• Graph traversals
• Divide and Conquers Algorithms
• Backtracking algorithms
• Tower of Hanoi

Backtracking:

Learn Backtracking to explore all the possible combinations to solve a problem and track back whenever we reach a dead-end.

Backtracking is a problem-solving algorithmic technique that involves finding a solution incrementally by trying  different options  and  undoing  them if they lead to a  dead end . It is commonly used in situations where you need to explore multiple possibilities to solve a problem, like searching for a path in a maze or solving puzzles like Sudoku. When a dead end is reached, the algorithm backtracks to the previous decision point and explores a different path until a solution is found or all possibilities have been exhausted.

Backtracking is used to solve problems which require exploring all the combinations or states. Some of the common problems which can be easily solved using backtracking are:

• N-Queen Problem
• Solve Sudoku
• M-coloring problem
• Rat in a Maze
• The Knight’s tour problem
• Permutation of given String
• Subset Sum problem
• Magnet Puzzle

Advanced Algorithms:

Bitwise algorithms:.

The  Bitwise Algorithms  is used to perform operations at the bit-level or to manipulate bits in different ways. The bitwise operations are found to be much faster and are sometimes used to improve the efficiency of a program. Bitwise algorithms  involve manipulating individual bits of binary representations of numbers to perform operations efficiently. These algorithms utilize bitwise operators like  AND, OR, XOR, shift operators , etc., to solve problems related to tasks such as setting, clearing, or toggling specific bits, checking if a number is even or odd, swapping values without using a temporary variable, and more.

Some of the most common problems based on Bitwise Algorithms are:

• Binary representation of a given number
• Count set bits in an integer
• Add two bit strings
• Turn off the rightmost set bit
• Rotate bits of a number
• Compute modulus division by a power-of-2-number
• Find the Number Occurring Odd Number of Times
• Program to find whether a given number is power of 2

Dynamic Programming:

Understand the concept of dynamic programming and how it can be applied to solve complex problems efficiently

Dynamic programming is a problem-solving technique used to solve problems by breaking them down into simpler subproblems. It is based on the principle of optimal substructure (optimal solution to a problem can be constructed from the optimal solutions of its subproblems) and overlapping subproblems (solutions to the same subproblems are needed repeatedly).

Dynamic programming is typically used to solve problems that can be divided into overlapping subproblems, such as those in the following categories:

• Optimization Problems : Problems where you need to find the best solution from a set of possible solutions. Examples include the shortest path problem, the longest common subsequence problem, and the knapsack problem.
• Counting Problems : Problems where you need to count the number of ways to achieve a certain goal. Examples include the number of ways to make change for a given amount of money and the number of ways to arrange a set of objects.
• Decision Problems : Problems where you need to make a series of decisions to achieve a certain goal. Examples include the traveling salesman problem and the 0/1 knapsack problem.

Dynamic programming can be applied to solve these problems efficiently by storing the solutions to subproblems in a table and reusing them when needed. This allows for the elimination of redundant computations and leads to significant improvements in time and space complexity.

The steps involved in solving a problem using dynamic programming are as follows:

• Identify the Subproblems : Break down the problem into smaller subproblems that can be solved independently.
• Define the Recurrence Relation : Define a recurrence relation that expresses the solution to the original problem in terms of the solutions to its subproblems.
• Solve the Subproblems : Solve the subproblems using the recurrence relation and store the solutions in a table.
• Build the Solution : Use the solutions to the subproblems to construct the solution to the original problem.
• Optimize : If necessary, optimize the solution by eliminating redundant computations or using space-saving techniques.

Greedy Algorithms:

Learn about greedy algorithms and their applications in optimization problems

Greedy algorithms are a class of algorithms that make a series of choices, each of which is the best at the moment, with the hope that this will lead to the best overall solution. They do not always guarantee an optimal solution, but they are often used because they are simple to implement and can be very efficient.

Here are some key points about greedy algorithms:

• Greedy Choice Property : A greedy algorithm makes a series of choices, each of which is the best at the moment, with the hope that this will lead to the best overall solution. This is known as the greedy choice property.
• Optimal Substructure : A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to its subproblems. Many problems that can be solved using greedy algorithms exhibit this property.
• Minimum Spanning Tree : In graph theory, a minimum spanning tree is a subset of the edges of a connected, edge-weighted graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.
• Shortest Path : In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.
• Huffman Encoding : Huffman encoding is a method of lossless data compression that assigns variable-length codes to input characters, with shorter codes assigned to more frequent characters.
• Greedy Choice Property : A greedy algorithm makes a series of choices, each of which is the best at the moment, with the hope that this will lead to the best overall solution.
• Optimal Substructure : A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to its subproblems.
• Greedy Algorithms are not always optimal : Greedy algorithms do not always guarantee an optimal solution, but they are often used because they are simple to implement and can be very efficient.
• Dijkstra's Algorithm : Dijkstra's algorithm is a graph search algorithm that finds the shortest path between two vertices in a graph with non-negative edge weights.
• Prim's Algorithm : Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph.

Divide and Conquer:

Understand the divide-and-conquer paradigm and how it is used in algorithms like merge sort and quicksort

Divide and conquer is a problem-solving paradigm that involves breaking a problem down into smaller subproblems, solving each subproblem independently, and then combining the solutions to the subproblems to solve the original problem. It is a powerful technique that is used in many algorithms, including merge sort and quicksort.

Here are the key steps involved in the divide-and-conquer paradigm:

• Divide : Break the problem down into smaller subproblems that are similar to the original problem but smaller in size.
• Conquer : Solve each subproblem independently using the same divide-and-conquer approach.
• Combine : Combine the solutions to the subproblems to solve the original problem.

Merge Sort:

• Divide : Divide the unsorted list into two sublists of about half the size.
• Conquer : Recursively sort each sublist.
• Combine : Merge the two sorted sublists into a single sorted list.
• Divide : Choose a pivot element from the list and partition the list into two sublists: elements less than the pivot and elements greater than the pivot.
• Combine : Combine the sorted sublists and the pivot element to form a single sorted list.

The divide-and-conquer paradigm is used in many algorithms because it can lead to efficient solutions for a wide range of problems. It is particularly useful for problems that can be divided into smaller subproblems that can be solved independently. By solving each subproblem independently and then combining the solutions, the divide-and-conquer approach can lead to a more efficient solution than solving the original problem directly.

Algorithm Analysis :

Learn about the time complexity and space complexity of algorithms and how to analyze them using Big O notation

Time complexity and space complexity are two important measures of the efficiency of an algorithm. They describe how the time and space requirements of an algorithm grow as the size of the input increases. Big O notation is a mathematical notation used to describe the upper bound on the growth rate of an algorithm's time or space requirements.

• Time complexity measures the amount of time an algorithm takes to run as a function of the size of the input.
• It is often expressed using Big O notation, which describes the upper bound on the growth rate of the algorithm's time requirements.
• For example, an algorithm with a time complexity of O(n) takes linear time, meaning the time it takes to run increases linearly with the size of the input.
• Common time complexities include O(1) (constant time), O(log n) (logarithmic time), O(n) (linear time), O(n log n) (linearithmic time), O(n^2) (quadratic time), O(n^3) (cubic time), and more.
• Space complexity measures the amount of memory an algorithm uses as a function of the size of the input.
• It is also expressed using Big O notation, which describes the upper bound on the growth rate of the algorithm's space requirements.
• For example, an algorithm with a space complexity of O(n) uses linear space, meaning the amount of memory it uses increases linearly with the size of the input.
• Common space complexities include O(1) (constant space), O(log n) (logarithmic space), O(n) (linear space), O(n log n) (linearithmic space), O(n^2) (quadratic space), O(n^3) (cubic space), and more.
• Identify the basic operations performed by the algorithm (e.g., comparisons, assignments, arithmetic operations).
• Determine the number of times each basic operation is performed as a function of the size of the input.
• Express the total number of basic operations as a mathematical function of the input size.
• Simplify the mathematical function and express it using Big O notation.
• The basic operations performed by the algorithm are comparisons and assignments.
• The number of comparisons is n - 1, and the number of assignments is 1.
• The total number of basic operations is 2n - 2.
• The time complexity of the algorithm is O(n), and the space complexity is O(1).

Understand the concepts of best-case, worst-case, and average-case time complexity.

The concepts of best-case, worst-case, and average-case time complexity are used to describe the performance of an algorithm under different scenarios. They help us understand how an algorithm behaves in different situations and provide insights into its efficiency.

• The best-case time complexity of an algorithm is the minimum amount of time it takes to run on any input of a given size.
• It represents the scenario where the algorithm performs optimally and takes the least amount of time to complete.
• Best-case time complexity is often denoted using Big O notation, where O(f(n)) represents the upper bound on the growth rate of the best-case running time as a function of the input size n.
• For example, an algorithm with a best-case time complexity of O(1) takes constant time, meaning it always completes in the same amount of time, regardless of the input size.
• The worst-case time complexity of an algorithm is the maximum amount of time it takes to run on any input of a given size.
• It represents the scenario where the algorithm performs the least efficiently and takes the most amount of time to complete.
• Worst-case time complexity is often denoted using Big O notation, where O(f(n)) represents the upper bound on the growth rate of the worst-case running time as a function of the input size n.
• For example, an algorithm with a worst-case time complexity of O(n^2) takes quadratic time, meaning the time it takes to run increases quadratically with the input size.
• The average-case time complexity of an algorithm is the average amount of time it takes to run on all possible inputs of a given size.
• It represents the expected performance of the algorithm when running on random inputs.
• Average-case time complexity is often denoted using Big O notation, where O(f(n)) represents the upper bound on the growth rate of the average-case running time as a function of the input size n.
• For example, an algorithm with an average-case time complexity of O(n) takes linear time, meaning the time it takes to run increases linearly with the input size.

Problem Solving :

Practice solving algorithmic problems on platforms like GeeksForGeeks , LeetCode, HackerRank, etc. GeeksforGeeks is a popular platform that provides a wealth of resources for learning and practicing problem-solving in computer science and programming. Here's how you can use GeeksforGeeks for problem-solving:

• Covers a wide range of topics, including data structures, algorithms, programming languages, databases, and more.
• Support for multiple programming languages. You can choose any language you're comfortable with or want to learn.
• Detailed explanations, examples, and implementations for various data structures and algorithms.
• Includes various approach to solve a problem starting from Brute Force to the most optimal approach.
• Interview Preparation section for common coding interview questions, tips and guidance.
• Discussion forum where users can ask and answer questions and engage in discussions to learn from others, seek help, and share your knowledge.
• Provides an online IDE for coding practice and experiment with code snippets, run them, and check the output directly on the platform.

To sharpen your data structures and algorithms knowledge, consider enrolling in the DSA to Development - Coding Guide course by GeeksforGeeks . This course offers a structured approach to learning DSA, providing you with the theoretical knowledge and practical skills needed to excel in both development and technical interviews. With hands-on exercises and expert guidance, this course will help you become a more proficient and confident developer. Explore the course to take your coding skills to the next level.

Why are Data Structure & Algorithms important in software development?

Data Structures and Algorithms are fundamental concepts in computer science and play a crucial role in software development for several reasons:

Additional Resources :

• Online Courses: Enroll in online courses on platforms like GeeksforGeeks, Coursera, edX, and Udemy.
• Practice: Solve coding challenges on websites like GeeksforGeeks, LeetCode, HackerRank, and CodeSignal.
• Community: Join online communities like GeeksforGeeks, Stack Overflow, Reddit, and GitHub to learn from others and share your knowledge.
• Books: Read books like "Introduction to Algorithms" by Cormen, Leiserson, Rivest, and Stein, and "Algorithms" by Robert Sedgewick and Kevin Wayne.

Similar Reads

• Data Structures & Algorithms Guide for Developers As a developer, understanding data structures and algorithms is crucial for writing efficient and scalable code. Here is a comprehensive guide to help you learn and master these fundamental concepts: Introduction to Algorithms and Data Structures (DSA):Data Structures and Algorithms are foundational 15+ min read
• Are Data Structures and Algorithms important for Web Developers? Web development is constantly changing, and new languages, technologies, and tools are emerging to help developers create engaging and functional web applications. Despite these additions, some basic concepts remain the same no matter what kind of development we are talking about, what language we’r 7 min read
• Is Data Structures and Algorithms Required for Android Development? Android development is a rapidly evolving field, with new technologies and tools constantly emerging. One question that often arises is whether a solid understanding of data structures and algorithms is necessary for Android developers. In this article, we will explore the importance of data structu 4 min read
• Why Every Developer Should Learn Data Structures and Algorithms? Software developers are regarded as the unknown heroes who design, execute, deploy and manage software programs. It is indeed a lucrative career option that promises insanely high salaries, amazing career growth, and global opportunities. As per the survey software development will witness an amazin 7 min read
• Data Structures and Algorithms (DSA) in C++ Data Structures and Algorithms (DSA) are fundamental part of computer science that allow you to store, organize, and process data in ways that maximize performance. This tutorial will guide you through the important data structures and key algorithms using C++ programming language. Why Learn DSA Usi 7 min read
• What Should I Learn First: Data Structures or Algorithms? Data structure and algorithms are an integral part of computer science. All the enthusiasts, at some point in time, learn these two important topics. They are different yet very much interrelated topics. This interrelation brings out the big question that needs to be answered: "What should I learn f 10 min read
• Learn Data Structures and Algorithms for Your Dream Job According to a study by employability assessment company Aspiring Minds in 2023, only 4.77 percent of candidates can write the correct logic for a program — a minimum requirement for any programming job. Another survey shows that only 7% of the engineering graduates in India are suitable for core en 8 min read
• Best Data Structures and Algorithms Books Data Structures and Algorithms is one of the most important skills that every Computer Science student must have. There are a number of remarkable publications on DSA in the market, with different difficulty levels, learning approaches and programming languages. In this article we're going to discus 9 min read
• Data Structures & Algorithms (DSA) Guide for Google Tech interviews Google is known for its rigorous and highly competitive technical interviews. These interviews are designed to assess a candidate's problem-solving abilities, technical knowledge, and cultural fit with the company. Preparing for technical interviews at top companies like Google requires a solid unde 9 min read
• DSA Tutorial - Learn Data Structures and Algorithms Data Structures and Algorithms (DSA) refer to the study of data structures used for organizing and storing data, along with the design of algorithms for solving problems that operate on these data structures. Why to Learn DSA?Whether it’s finding the shortest path in a GPS system or optimizing searc 8 min read
• Data Structures and Algorithms Online Courses : Free and Paid Data Structures and Algorithms is one of the most important skills that every computer science student must-have. It is often seen that people with good knowledge of these technologies are better programmers than others and thus, crack the interviews of almost every tech giant. Now, you must be thin 7 min read
• Real-life Applications of Data Structures and Algorithms (DSA) You may have heard that DSA is primarily used in the field of computer science. Although DSA is most commonly used in the computing field, its application is not restricted to it. The concept of DSA can also be found in everyday life. Here we'll address the common concept of DSA that we use in our d 10 min read
• How can one become good at Data structures and Algorithms easily? Let us first clarify the question. There is not any easy way to become good at anything but there is an efficient way to do everything. Let us try to understand the difference between easy and efficient here with the help of a programming question! Consider the problem of "Searching an element in a 4 min read
• Array Data Structure Guide In this article, we introduce array, implementation in different popular languages, its basic operations and commonly seen problems / interview questions. An array stores items (in case of C/C++ and Java Primitive Arrays) or their references (in case of Python, JS, Java Non-Primitive( at contiguous 4 min read
• Learn DSA in C: Master Data Structures and Algorithms Using C Data Structures and Algorithms (DSA) are one of the most important concepts of programming. They form the foundation of problem solving in computer science providing efficient solutions to the given problem that fits the requirement. This tutorial guide will help you understand the basics of various 8 min read
• Why Data Structures and Algorithms Are Important to Learn? Have you ever wondered why there's so much emphasis on learning data structures and algorithms (DSA) in programming? You might think, "Do I really need to know all this complicated stuff? It doesn't seem useful in real life." Let's dive into why understanding DSA is not just important but essential 4 min read
• What to do if I get stuck in Data Structures and Algorithms (DSA)? Learning Data Structures and Algorithms is like a big adventure where you explore various techniques that tell us how to solve complex problems in computer science. It's like solving a puzzle where you might not be sure what piece goes where. Thus there are times when you might feel stuck while lear 4 min read
• 10 Best Data Structures and Algorithms(DSA) Courses [2025] With advancement, it's important to walk with the trend. As you can see, the world is moving more towards IT, and everyone wants to upskill themselves with the best domains. And when we talk about the best IT domains, software development can't be ignored. One thing that you must have a good grip on 13 min read
• Walk-Through DSA3 : Data Structures and Algorithms Online Course by GeeksforGeeks This is a 10 weeks long online certification program specializing in Data Structures & Algorithms which includes pre-recorded premium Video lectures & programming questions for practice. You will learn algorithmic techniques for solving various computational problems and will implement more 5 min read

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Data Structures

Arrays - ds easy problem solving (basic) max score: 10 success rate: 92.99%, 2d array - ds easy problem solving (basic) max score: 15 success rate: 93.20%, dynamic array easy problem solving (basic) max score: 15 success rate: 87.12%, left rotation easy problem solving (basic) max score: 20 success rate: 91.64%, sparse arrays medium problem solving (basic) max score: 25 success rate: 97.30%, array manipulation hard problem solving (intermediate) max score: 60 success rate: 62.39%, print the elements of a linked list easy problem solving (basic) max score: 5 success rate: 97.10%, insert a node at the tail of a linked list easy problem solving (intermediate) max score: 5 success rate: 95.31%, insert a node at the head of a linked list easy problem solving (basic) max score: 5 success rate: 98.29%, insert a node at a specific position in a linked list easy problem solving (intermediate) max score: 5 success rate: 96.94%, cookie support is required to access hackerrank.

Seems like cookies are disabled on this browser, please enable them to open this website

Ace your Coding Interview

• DSA Problems
• Binary Tree
• Binary Search Tree
• Dynamic Programming
• Divide and Conquer
• Linked List
• Backtracking

Data Structures and Algorithms Problems

• TopClassic, TopLiked ↗ Easy
• TopLiked ↗ Medium
• TopLiked ↗ Easy
• TopClassic, TopLiked ↗ Medium
• ↗ Medium
• ↗ Hard
• ↗ Easy
• TopAlgo ↗ Easy
• TopClassic ↗ Medium
• TopAlgo, TopClassic, TopAlgo ↗ Easy
• TopLiked ↗ Hard
• TopClassic, TopLiked ↗ Hard
• TopClassic ↗ Hard
• TopClassic ↗ Easy
• TopAlgo ↗ Medium
• TopClassic Hard
• ↗ Beginner
• TopAlgo ↗ Hard
• TopLiked Medium
• TopClassic, TopLiked, TopDP ↗ Medium
• TopLiked, TopDP ↗ Hard
• TopClassic, TopLiked, TopDP ↗ Hard
• TopDP ↗ Medium
• TopAlgo Medium
• TopClassic Medium
• TopAlgo Hard

Rate this post

Average rating 4.88 /5. Vote count: 5940

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Tell us how we can improve this post?

Thanks for reading.

To share your code in the comments, please use our online compiler that supports C, C++, Java, Python, JavaScript, C#, PHP, and many more popular programming languages.

Like us? Refer us to your friends and support our growth. Happy coding :)

Learn Python practically and Get Certified .

Popular Tutorials

Popular examples, reference materials, certification courses.

Created with over a decade of experience and thousands of feedback.

Learn Data Structures and Algorithms

Recommended Course:

Learn DSA with Python

Perfect for beginners serious about building a career in DSA.

Created by the Programiz team with over a decade of experience.

• Enrollment: 7.4k
• Practice Problems: 101+
• Quizzes: 141+
• Certifications

Data Structures and Algorithms (DSA) is an essential skill for any programmer looking to solve problems efficiently.

Understanding and utilizing DSA is especially important when optimization is crucial, like in game development, live video apps, and other areas where even a one-second delay can impact performance.

Big companies tend to focus on DSA in coding interviews, so if you're good at it, you're more likely to land those higher-paying jobs.

In this guide, we will cover:

• Beginner's Guide to DSA
• Is DSA for You? (Hint: If you like breaking down problems and finding smart solutions, definitely yes!)
• Best Way to Learn DSA (Your way!)
• How to Practice DSA?

If you are simply looking to learn DSA step-by-step, you can follow our free tutorials in the next section.

Beginner's Guide to Data Structures and Algorithms

These tutorials will provide you with a solid foundation in Data Structures and Algorithms and prepare you for your career goals.

Getting Started with DSA

What is an algorithm?

Data Structure and Types

Why learn DSA?

Asymptotic Notations

Master Theorem

Divide and Conquer Algorithm

Types of Queue

Circular Queue

Priority Queue

Linked List

Linked List Operations

Types of Linked List

Heap Data Structure

Fibonacci Heap

Decrease Key and Delete Node Operations on a Fibonacci Heap

Tree Data Structure

Tree Traversal

Binary Tree

Full Binary Tree

Perfect Binary Tree

Complete Binary Tree

Balanced Binary Tree

Binary Search Tree

Insertion in a B-tree

Deletion from a B-tree

Insertion on a B+ Tree

Deletion from a B+ Tree

Red-Black Tree

Red-Black Tree Insertion

Deletion From a Red-Black Tree

Graph Data Structure

Spanning Tree

Strongly Connected Components

Adjacency Matrix

Adjacency List

DFS Algorithm

Breadth-first Search

Bellman Ford's Algorithm

Bubble Sort

Selection Sort

Insertion Sort

Counting Sort

Bucket Sort

Linear Search

Binary Search

Greedy Algorithm

Ford-Fulkerson Algorithm

Dijkstra's Algorithm

Kruskal's Algorithm

Prim's Algorithm

Huffman Coding

Dynamic Programming

Floyd-Warshall Algorithm

Longest Common Sequence

Backtracking Algorithm

Rabin-Karp Algorithm

Is DSA for you?

Whether DSA is the right choice depends on what you want to achieve in programming and your career goals.

DSA from Learning Perspective

If you're preparing for coding interviews, mastering Data Structures and Algorithms (DSA) is crucial. Most companies use DSA to test your problem-solving skills.

So learning DSA will boost your chances of landing a job.

Furthermore, if you're interested in performance-sensitive areas like game development, real-time data processing, or navigation apps (like Google Maps), learning DSA is crucial.

For example, the efficiency of a map application relies on the proper use of data structures and algorithms to quickly find the best routes.

Even if you're not focused on performance-sensitive fields, a basic knowledge of DSA is still important. It helps you write cleaner, more efficient code and lays the foundation for building scalable applications.

DSA is essential for anyone who wants to excel in programming.

DSA as a Career Choice

Data Structures and Algorithms (DSA) are fundamental for creating efficient and optimized software solutions. It's used in:

• Software Development
• System Design
• Data Engineering
• Algorithmic Trading
• Competitive Programming and more

However, there are certain fields where focusing heavily on DSA might not be as essential. For example, if you are primarily interested in frontend design, UX/UI development, or simple scripting tasks, then deep DSA knowledge might not be your top priority.

In these cases, skills such as design principles, creativity, or proficiency in specific tools like HTML/CSS for frontend design or Python for scripting might be more relevant.

Ultimately, your career goals will help determine how important DSA is for you.

Best Way to Learn DSA

There is no right or wrong way to learn DSA. It all depends on your learning style and pace.

In this section, we have included the best DSA learning resources tailored to your learning preferences, be it text-based, video-based, or interactive courses.

Text-based Tutorial

Best: if you are committed to learning DSA but do not want to spend on it.

If you want to learn DSA for free with a well-organized, step-by-step tutorial, you can use our free DSA tutorials .

Our tutorials will guide you through DSA one step at a time, using practical examples to strengthen your foundation.

Interactive Course

Best: if you want hands-on learning, get your progress tracked, and maintain a learning streak.

Learning to code is tough. It requires dedication and consistency, and you need to write tons of code yourself.

While videos and tutorials provide you with a step-by-step guide, they lack hands-on experience and structure.

Recognizing all these challenges, Programiz offers a premium DSA Interactive Course that allows you to gain hands-on learning experience by solving problems, building real-world projects, and tracking your progress.

Best: if you want to have in-depth understanding at your own pace.

Books are a great way to learn. They give you a comprehensive view of programming concepts that you might not get elsewhere.

Here are some books we personally recommend:

• Introduction to Algorithms, Thomas H. Cormen
• Algorithms, Robert Sedgewick
• The Art of Computer Programming, Donald E. Knuth

Visualization

Best: if you're a visual learner who grasps concepts better by seeing them in action.

Once you have some idea about data structure and algorithms, there is a great resource at Data Structure Visualizations that lets you learn through animation. There are many visualizer tools, however you can use Data Structure Visualization (usfca.edu) .

Important: You cannot learn DSA without developing the habit of practicing it yourself. Therefore, whatever method you choose, always work on DSA problems.

While solving problems, you will encounter challenges. Don't worry about them; try to understand them and find solutions. Remember, mastering DSA is all about solving problems, and difficulties are part of the process.

How to Get Started with DSA?

Practice DSA on Your Computer.

As you move forward with more advanced algorithms and complex data structures, practicing DSA problems on your local machine becomes essential. This hands-on practice will help you apply what you've learned and build confidence in solving problems efficiently.

To learn how to get started with DSA concepts and practice them effectively, follow our detailed guide.

Learn the core concepts and techniques in DSA that will help you solve complex programming problems efficiently.