research and null hypothesis examples

15 Null Hypothesis Examples

Chris Drew (PhD)

Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]

Learn about our Editorial Process

A null hypothesis is a general assertion or default position that there is no relationship or effect between two measured phenomena.

It’s a critical part of statistics, data analysis, and the scientific method . This concept forms the basis of testing statistical significance and allows researchers to be objective in their conclusions.

A null hypothesis helps to eliminate biases and ensures that the observed results are not due to chance. The rejection or failure to reject the null hypothesis helps in guiding the course of research.

Null Hypothesis Definition

The null hypothesis, often denoted as H 0 , is the hypothesis in a statistical test which proposes no statistical significance exists in a set of observed data.

It hypothesizes that any kind of difference or importance you see in a data set is due to chance.

Null hypotheses are typically proposed to be negated or disproved by statistical tests, paving way for the acceptance of an alternate hypothesis.

Importantly, a null hypothesis cannot be proven true; it can only be supported or rejected with confidence.

Should evidence – via statistical analysis – contradict the null hypothesis, it is rejected in favor of an alternative hypothesis. In essence, the null hypothesis is a tool to challenge and disprove that there is no effect or relationship between variables.

Video Explanation

I like to show this video to my students which outlines a null hypothesis really clearly and engagingly, using real life studies by research students! The into explains it really well:

“There’s an idea in science called the null hypothesis and it works like this: when you’re setting out to prove a theory, your default answer should be “it’s not going to work” and you have to convince the world otherwise through clear results”

Here’s the full video:

Null Hypothesis Examples

• Equality of Means: The null hypothesis posits that the average of group A does not differ from the average of group B. It suggests that any observed difference between the two group means is due to sampling or experimental error.
• No Correlation: The null hypothesis states there is no correlation between the variable X and variable Y in the population. It means that any correlation seen in sample data occurred by chance.
• Drug Effectiveness: The null hypothesis proposes that a new drug does not reduce the number of days to recover from a disease compared to a standard drug. Any observed difference is merely by chance and not due to the new drug.
• Classroom Teaching Method: The null hypothesis states that a new teaching method does not result in improved test scores compared to the traditional teaching method. Any improvement in scores can be attributed to chance or other unrelated factors.
• Smoking and Life Expectancy: The null hypothesis asserts that the average life expectancy of smokers is the same as that of non-smokers. Any perceived difference in life expectancy is due to random variation or other factors.
• Brand Preference: The null hypothesis suggests that the proportion of consumers preferring Brand A is the same as those preferring Brand B. Any observed preference in the sample is due to random selection.
• Vaccination Efficacy: The null hypothesis states that the efficacy of Vaccine A does not differ from that of Vaccine B. Any differences observed in a sample are due to chance or other confounding factors.
• Diet and Weight Loss: The null hypothesis proposes that following a specific diet does not result in more weight loss than not following the diet. Any weight loss observed among dieters is considered random or influenced by other factors.
• Exercise and Heart Rate: The null hypothesis states that regular exercise does not lower resting heart rate compared to no exercise. Any lower heart rates observed in exercisers could be due to chance or other unrelated factors.
• Climate Change: The null hypothesis asserts that the average global temperature this decade is not higher than the previous decade. Any observed temperature increase can be attributed to random variation or unaccounted factors.
• Gender Wage Gap: The null hypothesis posits that men and women earn the same average wage for the same job. Any observed wage disparity is due to chance or non-gender related factors.
• Psychotherapy Effectiveness: The null hypothesis states that patients undergoing psychotherapy do not show more improvement than those not undergoing therapy. Any improvement in the
• Energy Drink Consumption and Sleep: The null hypothesis proposes that consuming energy drinks does not affect the quantity of sleep. Any observed differences in sleep duration among energy drink consumers is due to random variation or other factors.
• Organic Food and Health: The null hypothesis asserts that consuming organic food does not lead to better health outcomes compared to consuming non-organic food. Any health differences observed in consumers of organic food are considered random or attributed to other confounding factors.
• Online Learning Effectiveness: The null hypothesis states that students learning online do not perform differently on exams than students learning in traditional classrooms. Any difference in performance can be attributed to chance or unrelated factors.

Null Hypothesis vs Alternative Hypothesis

An alternative hypothesis is the direct contrast to the null hypothesis. It posits that there is a statistically significant relationship or effect between the variables being observed.

If the null hypothesis is rejected based on the test data, the alternative hypothesis is accepted.

Importantly, while the null hypothesis is typically a statement of ‘no effect’ or ‘no difference,’ the alternative hypothesis states that there is an effect or difference.

Comprehension Checkpoint: How does the null hypothesis help to ensure that research is objective and unbiased?

Applications of the Null Hypothesis in Research

The null hypothesis plays a critical role in numerous research settings, promoting objectivity and ensuring findings aren’t due to random chance.

• Clinical Trials: Null hypothesis is used extensively in medical and pharmaceutical research. For example, when testing a new drug’s effectiveness, the null hypothesis might state that the drug has no effect on the disease. If data contradicts this, the null hypothesis is rejected, suggesting the drug might be effective.
• Business and Economics: Businesses use null hypotheses to make informed decisions. For instance, a company might use a null hypothesis to test if a new marketing strategy improves sales. If data suggests a significant increase in sales, the null hypothesis is rejected, and the new strategy may be implemented.
• Psychological Research: Psychologists use null hypotheses to test theories about behavior. For instance, a null hypothesis might state there’s no link between stress and sleep quality. Rejecting this hypothesis based on collected data could help establish a correlation between the two variables.
• Environmental Science: Null hypotheses are used to understand environmental changes. For instance, researchers might form a null hypothesis stating there is no significant difference in air quality before and after a policy change. If this hypothesis is rejected, it indicates the policy may have impacted air quality.
• Education: Educators and researchers often use null hypotheses to improve teaching methods. For example, a null hypothesis might propose a new teaching technique doesn’t enhance student performance. If data contradicts this, the technique may be beneficial.

In all these areas, the null hypothesis helps minimize bias, enabling researchers to support their findings with statistically significant data. It forms the backbone of many scientific research methodologies , promoting a disciplined approach to uncovering new knowledge.

See More Hypothesis Examples Here

The null hypothesis is a cornerstone of statistical analysis and empirical research. It serves as a starting point for investigations, providing a baseline premise that the observed effects are due to chance. By understanding and applying the concept of the null hypothesis, researchers can test the validity of their assumptions, making their findings more robust and reliable. In essence, the null hypothesis ensures that the scientific exploration remains objective, systematic, and free from unintended bias.

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ Free Social Skills Worksheets
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 10 Reasons you’re Perpetually Single
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 20 Montessori Toddler Bedrooms (Design Inspiration)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 21 Montessori Homeschool Setups

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Null Hypothesis Examples

The null hypothesis (H 0 ) is the hypothesis that states there is no statistical difference between two sample sets. In other words, it assumes the independent variable does not have an effect on the dependent variable in a scientific experiment .

The null hypothesis is the most powerful type of hypothesis in the scientific method because it’s the easiest one to test with a high confidence level using statistics. If the null hypothesis is accepted, then it’s evidence any observed differences between two experiment groups are due to random chance. If the null hypothesis is rejected, then it’s strong evidence there is a true difference between test sets or that the independent variable affects the dependent variable.

• The null hypothesis is a nullifiable hypothesis. A researcher seeks to reject it because this result strongly indicates observed differences are real and not just due to chance.
• The null hypothesis may be accepted or rejected, but not proven. There is always a level of confidence in the outcome.

What Is the Null Hypothesis?

The null hypothesis is written as H 0 , which is read as H-zero, H-nought, or H-null. It is associated with another hypothesis, called the alternate or alternative hypothesis H A or H 1 . When the null hypothesis and alternate hypothesis are written mathematically, they cover all possible outcomes of an experiment.

An experimenter tests the null hypothesis with a statistical analysis called a significance test. The significance test determines the likelihood that the results of the test are not due to chance. Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01). But, even if the confidence in the test is high, there is always a small chance the outcome is incorrect. This means you can’t prove a null hypothesis. It’s also a good reason why it’s important to repeat experiments.

Exact and Inexact Null Hypothesis

The most common type of null hypothesis assumes no difference between two samples or groups or no measurable effect of a treatment. This is the exact hypothesis . If you’re asked to state a null hypothesis for a science class, this is the one to write. It is the easiest type of hypothesis to test and is the only one accepted for certain types of analysis. Examples include:

There is no difference between two groups H 0 : μ 1  = μ 2 (where H 0  = the null hypothesis, μ 1  = the mean of population 1, and μ 2  = the mean of population 2)

Both groups have value of 100 (or any number or quality) H 0 : μ = 100

However, sometimes a researcher may test an inexact hypothesis . This type of hypothesis specifies ranges or intervals. Examples include:

Recovery time from a treatment is the same or worse than a placebo: H 0 : μ ≥ placebo time

There is a 5% or less difference between two groups: H 0 : 95 ≤ μ ≤ 105

An inexact hypothesis offers “directionality” about a phenomenon. For example, an exact hypothesis can indicate whether or not a treatment has an effect, while an inexact hypothesis can tell whether an effect is positive of negative. However, an inexact hypothesis may be harder to test and some scientists and statisticians disagree about whether it’s a true null hypothesis .

How to State the Null Hypothesis

To state the null hypothesis, first state what you expect the experiment to show. Then, rephrase the statement in a form that assumes there is no relationship between the variables or that a treatment has no effect.

Example: A researcher tests whether a new drug speeds recovery time from a certain disease. The average recovery time without treatment is 3 weeks.

• State the goal of the experiment: “I hope the average recovery time with the new drug will be less than 3 weeks.”
• Rephrase the hypothesis to assume the treatment has no effect: “If the drug doesn’t shorten recovery time, then the average time will be 3 weeks or longer.” Mathematically: H 0 : μ ≥ 3

This null hypothesis (inexact hypothesis) covers both the scenario in which the drug has no effect and the one in which the drugs makes the recovery time longer. The alternate hypothesis is that average recovery time will be less than three weeks:

H A : μ < 3

Of course, the researcher could test the no-effect hypothesis (exact null hypothesis): H 0 : μ = 3

The danger of testing this hypothesis is that rejecting it only implies the drug affected recovery time (not whether it made it better or worse). This is because the alternate hypothesis is:

H A : μ ≠ 3 (which includes μ <3 and μ >3)

Even though the no-effect null hypothesis yields less information, it’s used because it’s easier to test using statistics. Basically, testing whether something is unchanged/changed is easier than trying to quantify the nature of the change.

Remember, a researcher hopes to reject the null hypothesis because this supports the alternate hypothesis. Also, be sure the null and alternate hypothesis cover all outcomes. Finally, remember a simple true/false, equal/unequal, yes/no exact hypothesis is easier to test than a more complex inexact hypothesis.

• Adèr, H. J.; Mellenbergh, G. J. & Hand, D. J. (2007).  Advising on Research Methods: A Consultant’s Companion . Huizen, The Netherlands: Johannes van Kessel Publishing. ISBN  978-90-79418-01-5 .
• Cox, D. R. (2006).  Principles of Statistical Inference . Cambridge University Press. ISBN  978-0-521-68567-2 .
• Everitt, Brian (1998).  The Cambridge Dictionary of Statistics . Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
• Weiss, Neil A. (1999).  Introductory Statistics  (5th ed.). ISBN 9780201598773.

Related Posts

• Science, Tech, Math ›
• Chemistry ›
• Chemical Laws ›

Null Hypothesis Definition and Examples

PM Images / Getty Images

• Chemical Laws
• Periodic Table
• Projects & Experiments
• Scientific Method
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In a scientific experiment, the null hypothesis is the proposition that there is no effect or no relationship between phenomena or populations. If the null hypothesis is true, any observed difference in phenomena or populations would be due to sampling error (random chance) or experimental error. The null hypothesis is useful because it can be tested and found to be false, which then implies that there is a relationship between the observed data. It may be easier to think of it as a nullifiable hypothesis or one that the researcher seeks to nullify. The null hypothesis is also known as the H 0, or no-difference hypothesis.

The alternate hypothesis, H A or H 1 , proposes that observations are influenced by a non-random factor. In an experiment, the alternate hypothesis suggests that the experimental or independent variable has an effect on the dependent variable .

How to State a Null Hypothesis

There are two ways to state a null hypothesis. One is to state it as a declarative sentence, and the other is to present it as a mathematical statement.

For example, say a researcher suspects that exercise is correlated to weight loss, assuming diet remains unchanged. The average length of time to achieve a certain amount of weight loss is six weeks when a person works out five times a week. The researcher wants to test whether weight loss takes longer to occur if the number of workouts is reduced to three times a week.

The first step to writing the null hypothesis is to find the (alternate) hypothesis. In a word problem like this, you're looking for what you expect to be the outcome of the experiment. In this case, the hypothesis is "I expect weight loss to take longer than six weeks."

This can be written mathematically as: H 1 : μ > 6

In this example, μ is the average.

Now, the null hypothesis is what you expect if this hypothesis does not happen. In this case, if weight loss isn't achieved in greater than six weeks, then it must occur at a time equal to or less than six weeks. This can be written mathematically as:

H 0 : μ ≤ 6

The other way to state the null hypothesis is to make no assumption about the outcome of the experiment. In this case, the null hypothesis is simply that the treatment or change will have no effect on the outcome of the experiment. For this example, it would be that reducing the number of workouts would not affect the time needed to achieve weight loss:

H 0 : μ = 6

Null Hypothesis Examples

"Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a null hypothesis.

Another example of a null hypothesis is "Plant growth rate is unaffected by the presence of cadmium in the soil ." A researcher could test the hypothesis by measuring the growth rate of plants grown in a medium lacking cadmium, compared with the growth rate of plants grown in mediums containing different amounts of cadmium. Disproving the null hypothesis would set the groundwork for further research into the effects of different concentrations of the element in soil.

Why Test a Null Hypothesis?

You may be wondering why you would want to test a hypothesis just to find it false. Why not just test an alternate hypothesis and find it true? The short answer is that it is part of the scientific method. In science, propositions are not explicitly "proven." Rather, science uses math to determine the probability that a statement is true or false. It turns out it's much easier to disprove a hypothesis than to positively prove one. Also, while the null hypothesis may be simply stated, there's a good chance the alternate hypothesis is incorrect.

For example, if your null hypothesis is that plant growth is unaffected by duration of sunlight, you could state the alternate hypothesis in several different ways. Some of these statements might be incorrect. You could say plants are harmed by more than 12 hours of sunlight or that plants need at least three hours of sunlight, etc. There are clear exceptions to those alternate hypotheses, so if you test the wrong plants, you could reach the wrong conclusion. The null hypothesis is a general statement that can be used to develop an alternate hypothesis, which may or may not be correct.

• Kelvin Temperature Scale Definition
• Independent Variable Definition and Examples
• Theory Definition in Science
• Hypothesis Definition (Science)
• de Broglie Equation Definition
• Law of Combining Volumes Definition
• Chemical Definition
• Pure Substance Definition in Chemistry
• Acid Definition and Examples
• Extensive Property Definition (Chemistry)
• Radiation Definition and Examples
• Valence Definition in Chemistry
• Atomic Solid Definition
• Weak Base Definition and Examples
• Oxidation Definition and Example in Chemistry
• Definition of Binary Compound

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

Null Hypothesis

Ai generator.

Making a certain class or laboratory experiment would require a good null hypothesis . You will be given variables to be used in your experiment and then you would be able to identify the relationship between the two. Every beginning of the experiment report would indicate your hypotheses. It is proven useful for it can be tested to prove if the result is considered false.

What is a Null Hypothesis?

A null hypothesis is used during experiments to prove that there is no difference in the relationship between the two variables. Every type of experiment would require you to make a null hypothesis. From the word itself “null” means zero or no value. If you want to practice making a good experiment report , consider providing a good null hypothesis. Null hypothesis is designed to be rejected if the alternative hypothesis is proven to be exact.

Null Hypothesis Examples in Research

1. medical research.

• Research Question: Does a new drug lower cholesterol levels more effectively than the current drug?
• Null Hypothesis (H0): The new drug has no effect on cholesterol levels compared to the current drug.
• Symbolic Form: H0: ?1 = ?2

2. Educational Research

• Research Question: Does the use of interactive technology improve student test scores?
• Null Hypothesis (H0): Interactive technology does not improve student test scores.

3. Business Research

• Research Question: Does a new marketing strategy increase sales?
• Null Hypothesis (H0): The new marketing strategy does not increase sales.

4. Psychological Research

• Research Question: Does cognitive-behavioral therapy reduce symptoms of anxiety more than standard therapy?
• Null Hypothesis (H0): Cognitive-behavioral therapy does not reduce anxiety symptoms more than standard therapy.

5. Environmental Research

• Research Question: Does urbanization affect bird population diversity?
• Null Hypothesis (H0): Urbanization has no effect on bird population diversity.
• Symbolic Form: H0: ?urban = ?rural

6. Nutritional Research

• Research Question: Does a low-carb diet lead to more weight loss than a low-fat diet?
• Null Hypothesis (H0): A low-carb diet does not lead to more weight loss than a low-fat diet.

7. Economic Research

• Research Question: Does increasing the minimum wage reduce poverty levels?
• Null Hypothesis (H0): Increasing the minimum wage does not reduce poverty levels.
• Symbolic Form: H0: ?before = ?after

8. Sociological Research

• Research Question: Does social media usage affect teenagers’ self-esteem?
• Null Hypothesis (H0): Social media usage does not affect teenagers’ self-esteem.
• Symbolic Form: H0: ?users = ?non-users

9. Agricultural Research

• Research Question: Does the use of a new fertilizer increase crop yield?
• Null Hypothesis (H0): The new fertilizer does not increase crop yield.

10. Technological Research

• Research Question: Does a new software algorithm improve processing speed?
• Null Hypothesis (H0): The new software algorithm does not improve processing speed.
• Symbolic Form: H0: ?new = ?old

Null Hypothesis Examples in Psychology

1. effectiveness of therapy.

• Research Question: Does cognitive-behavioral therapy (CBT) reduce symptoms of depression more effectively than no treatment?
• Null Hypothesis (H0): Cognitive-behavioral therapy does not reduce symptoms of depression more effectively than no treatment.
• Symbolic Form: H0: ?CBT = ?control

2. Impact of Sleep on Memory

• Research Question: Does sleep deprivation affect short-term memory performance?
• Null Hypothesis (H0): Sleep deprivation has no effect on short-term memory performance.
• Symbolic Form: H0: ?sleep_deprived = ?non_sleep_deprived

3. Influence of Color on Mood

• Research Question: Does the color of a room affect individuals’ mood?
• Null Hypothesis (H0): The color of a room does not affect individuals’ mood.
• Symbolic Form: H0: ?color1 = ?color2 = ?color3

4. Social Media and Self-Esteem

• Research Question: Does the frequency of social media use affect teenagers’ self-esteem?
• Null Hypothesis (H0): The frequency of social media use does not affect teenagers’ self-esteem.
• Symbolic Form: H0: ?high_use = ?low_use

5. Mindfulness and Stress Reduction

• Research Question: Does mindfulness meditation reduce stress levels in college students?
• Null Hypothesis (H0): Mindfulness meditation does not reduce stress levels in college students.
• Symbolic Form: H0: ?mindfulness = ?control

6. Parenting Styles and Academic Performance

• Research Question: Does authoritative parenting style affect children’s academic performance?
• Null Hypothesis (H0): Authoritative parenting style does not affect children’s academic performance.
• Symbolic Form: H0: ?authoritative = ?other_styles

7. Impact of Exercise on Anxiety

• Research Question: Does regular exercise reduce anxiety levels in adults?
• Null Hypothesis (H0): Regular exercise does not reduce anxiety levels in adults.
• Symbolic Form: H0: ?exercise = ?no_exercise

8. Gender Differences in Risk-Taking Behavior

• Research Question: Are there differences in risk-taking behavior between males and females?
• Null Hypothesis (H0): There are no differences in risk-taking behavior between males and females.
• Symbolic Form: H0: ?males = ?females

9. Impact of Music on Concentration

• Research Question: Does listening to music while studying affect concentration levels?
• Null Hypothesis (H0): Listening to music while studying does not affect concentration levels.
• Symbolic Form: H0: ?music = ?no_music

10. Effect of Group Therapy on Social Skills

• Research Question: Does group therapy improve social skills in individuals with social anxiety?
• Null Hypothesis (H0): Group therapy does not improve social skills in individuals with social anxiety.
• Symbolic Form: H0: ?group_therapy = ?no_therapy

Null Hypothesis Examples in Biology

1. effect of fertilizers on plant growth.

• Research Question: Does a new fertilizer improve plant growth compared to no fertilizer?
• Null Hypothesis (H0): The new fertilizer does not improve plant growth compared to no fertilizer.
• Symbolic Form: H0: ?fertilizer = ?no_fertilizer

2. Antibiotic Effectiveness on Bacteria

• Research Question: Does a new antibiotic reduce bacterial growth more effectively than an existing antibiotic?
• Null Hypothesis (H0): The new antibiotic does not reduce bacterial growth more effectively than the existing antibiotic.
• Symbolic Form: H0: ?new_antibiotic = ?existing_antibiotic

3. Impact of Temperature on Enzyme Activity

• Research Question: Does temperature affect the activity of a specific enzyme?
• Null Hypothesis (H0): Temperature does not affect the activity of the specific enzyme.
• Symbolic Form: H0: Enzyme activity at temperature1 = Enzyme activity at temperature2

4. Genetic Influence on Trait Expression

• Research Question: Does a specific gene affect the expression of a particular trait in a plant species?
• Null Hypothesis (H0): The specific gene does not affect the expression of the particular trait in the plant species.
• Symbolic Form: H0: Trait expression with gene = Trait expression without gene

5. Effect of Light Intensity on Photosynthesis

• Research Question: Does light intensity affect the rate of photosynthesis in plants?
• Null Hypothesis (H0): Light intensity does not affect the rate of photosynthesis in plants.
• Symbolic Form: H0: Photosynthesis rate at light intensity1 = Photosynthesis rate at light intensity2

6. Impact of Diet on Animal Growth

• Research Question: Does a high-protein diet affect the growth rate of animals?
• Null Hypothesis (H0): A high-protein diet does not affect the growth rate of animals.
• Symbolic Form: H0: Growth rate on high-protein diet = Growth rate on normal diet

7. Effect of Pollution on Aquatic Life

• Research Question: Does water pollution affect the survival rate of fish in a lake?
• Null Hypothesis (H0): Water pollution does not affect the survival rate of fish in a lake.
• Symbolic Form: H0: Fish survival in polluted water = Fish survival in non-polluted water

8. Impact of Caffeine on Heart Rate in Daphnia

• Research Question: Does caffeine affect the heart rate of Daphnia (water fleas)?
• Null Hypothesis (H0): Caffeine does not affect the heart rate of Daphnia.
• Symbolic Form: H0: Heart rate with caffeine = Heart rate without caffeine

9. Influence of Soil pH on Plant Germination

• Research Question: Does soil pH affect the germination rate of seeds?
• Null Hypothesis (H0): Soil pH does not affect the germination rate of seeds.
• Symbolic Form: H0: Germination rate at pH1 = Germination rate at pH2

10. Effect of Salinity on Aquatic Plant Growth

• Research Question: Does salinity affect the growth of aquatic plants?
• Null Hypothesis (H0): Salinity does not affect the growth of aquatic plants.
• Symbolic Form: H0: Plant growth in saline water = Plant growth in freshwater

Null Hypothesis Examples in Business

1. effect of marketing campaign on sales.

• Research Question: Does a new marketing campaign increase product sales?
• Null Hypothesis (H0): The new marketing campaign does not increase product sales.
• Symbolic Form: H0: ?campaign = ?no_campaign

2. Impact of Training Programs on Employee Productivity

• Research Question: Do training programs improve employee productivity?
• Null Hypothesis (H0): Training programs do not improve employee productivity.
• Symbolic Form: H0: ?trained = ?untrained

3. Influence of Price Changes on Demand

• Research Question: Do price changes affect the demand for a product?
• Null Hypothesis (H0): Price changes do not affect the demand for the product.
• Symbolic Form: H0: ?price_change = ?no_price_change

4. Customer Satisfaction and Service Quality

• Research Question: Does improving service quality increase customer satisfaction?
• Null Hypothesis (H0): Improving service quality does not increase customer satisfaction.
• Symbolic Form: H0: ?improved_service = ?standard_service

5. Effect of Employee Benefits on Retention Rates

• Research Question: Do enhanced employee benefits reduce turnover rates?
• Null Hypothesis (H0): Enhanced employee benefits do not reduce turnover rates.
• Symbolic Form: H0: ?enhanced_benefits = ?standard_benefits

6. Impact of Social Media Presence on Brand Awareness

• Research Question: Does an active social media presence increase brand awareness?
• Null Hypothesis (H0): An active social media presence does not increase brand awareness.
• Symbolic Form: H0: ?active_social_media = ?inactive_social_media

7. Influence of Store Layout on Customer Purchases

• Research Question: Does store layout affect customer purchasing behavior?
• Null Hypothesis (H0): Store layout does not affect customer purchasing behavior.
• Symbolic Form: H0: ?layout1 = ?layout2

8. Online Advertising and Website Traffic

• Research Question: Does online advertising increase website traffic?
• Null Hypothesis (H0): Online advertising does not increase website traffic.
• Symbolic Form: H0: ?ads = ?no_ads

9. Effect of Product Packaging on Sales

• Research Question: Does new product packaging design increase sales?
• Null Hypothesis (H0): The new product packaging design does not increase sales.
• Symbolic Form: H0: ?new_packaging = ?old_packaging

10. Influence of Remote Work on Employee Performance

• Research Question: Does remote work affect employee performance?
• Null Hypothesis (H0): Remote work does not affect employee performance.
• Symbolic Form: H0: ?remote_work = ?office_work

Null Hypothesis Examples in Statistics

1. comparing means.

• Research Question: Is there a difference in average test scores between two groups of students?
• Null Hypothesis (H0): There is no difference in the average test scores between the two groups.

2. Proportions

• Research Question: Is the proportion of defective products the same in two different production lines?
• Null Hypothesis (H0): The proportion of defective products is the same in both production lines.
• Symbolic Form: H0: p1 = p2

3. Regression Analysis

• Research Question: Is there a relationship between years of experience and salary?
• Null Hypothesis (H0): There is no relationship between years of experience and salary.
• Symbolic Form: H0: ? = 0 (where ? is the regression coefficient)

4. ANOVA (Analysis of Variance)

• Research Question: Are the means of three or more groups equal?
• Null Hypothesis (H0): The means of all groups are equal.
• Symbolic Form: H0: ?1 = ?2 = ?3 = … = ?k

5. Chi-Square Test for Independence

• Research Question: Are gender and voting preference independent?
• Null Hypothesis (H0): Gender and voting preference are independent.
• Symbolic Form: H0: There is no association between gender and voting preference.

6. Time Series Analysis

• Research Question: Does a time series exhibit a trend over time?
• Null Hypothesis (H0): There is no trend in the time series data over time.
• Symbolic Form: H0: The time series has no significant trend component.

7. Hypothesis Testing for Variance

• Research Question: Is the variance in test scores different between two classes?
• Null Hypothesis (H0): The variances in test scores are equal between the two classes.
• Symbolic Form: H0: ?1² = ?2²

8. Correlation Analysis

• Research Question: Is there a correlation between two variables, such as height and weight?
• Null Hypothesis (H0): There is no correlation between the two variables.
• Symbolic Form: H0: ? = 0 (where ? is the correlation coefficient)

9. Two-Sample t-Test

• Research Question: Do two samples have the same mean?
• Null Hypothesis (H0): The two samples have the same mean.

10. One-Sample t-Test

• Research Question: Does the sample mean differ from a known population mean?
• Null Hypothesis (H0): The sample mean is equal to the population mean.
• Symbolic Form: H0: ? = ?0

Real life Examples of Null Hypothesis

1. medical studies.

• Research Question: Does a new medication lower blood pressure more effectively than the current medication?
• Null Hypothesis (H0): The new medication does not lower blood pressure more effectively than the current medication.
• Example: A clinical trial compares blood pressure readings between patients taking the new medication and those taking the current medication.

2. Education

• Research Question: Does a new teaching method improve student test scores?
• Null Hypothesis (H0): The new teaching method does not improve student test scores.
• Example: An educational study compares test scores of students taught using the new method versus those taught using traditional methods.

3. Business

• Research Question: Does a new advertising campaign increase product sales?
• Null Hypothesis (H0): The new advertising campaign does not increase product sales.
• Example: A company runs the new campaign and compares sales data before and after the campaign.

4. Public Health

• Research Question: Does a smoking cessation program reduce the smoking rate in a community?
• Null Hypothesis (H0): The smoking cessation program does not reduce the smoking rate in the community.
• Example: Public health officials analyze smoking rates before and after implementing the program.

5. Environmental Science

• Research Question: Does the introduction of a specific fish species affect the biodiversity of a lake?
• Null Hypothesis (H0): The introduction of the specific fish species does not affect the biodiversity of the lake.
• Example: Environmental scientists monitor biodiversity levels before and after introducing the fish species.

6. Economics

• Research Question: Does raising the minimum wage reduce poverty levels?
• Null Hypothesis (H0): Raising the minimum wage does not reduce poverty levels.
• Example: Economists compare poverty rates in regions with and without recent minimum wage increases.

7. Psychology

• Research Question: Does mindfulness meditation reduce stress levels among college students?
• Null Hypothesis (H0): Mindfulness meditation does not reduce stress levels among college students.
• Example: A study measures stress levels before and after a mindfulness meditation program in a group of students.

8. Agriculture

• Example: Farmers apply the new fertilizer to one field and a standard fertilizer to another and compare the yields.

9. Technology

• Research Question: Does a new software update improve the speed of a computer program?
• Null Hypothesis (H0): The new software update does not improve the speed of the computer program.
• Example: Software engineers measure the program’s speed before and after applying the update.

10. Marketing

• Research Question: Does personalized email marketing increase customer engagement?
• Null Hypothesis (H0): Personalized email marketing does not increase customer engagement.
• Example: A company sends personalized emails to one group and generic emails to another, then compares engagement rates.

More Null Hypothesis Examples & Samples in PDF

1. null hypothesis significance test example.

2. Sample Null Hypothesis Example

3. Critical Assessment of Null Hypothesis Example

4. Confidence Levels for Null Hypotheses Example

5. Interpreting Failure to Reject A Null Hypothesis Example

6. Simple Null Hypothesis Example

7. Basic Neurology Null Hypothesis Example

8. Null Research Hypothesis in DOC

Purpose of Null Hypothesis

The null hypothesis is a fundamental concept in statistics and scientific research . It serves several critical purposes in the process of hypothesis testing, guiding researchers in drawing meaningful conclusions from their data. Below are the primary purposes of the null hypothesis:

1. Baseline for Comparison

The null hypothesis provides a baseline or a default position that indicates no effect, no difference, or no relationship between variables. It is the statement that researchers aim to test against an alternative hypothesis. By starting with the assumption that there is no effect, researchers can objectively assess whether the data provide enough evidence to support the alternative hypothesis.

2. Eliminates Bias

By assuming no effect or no difference, the null hypothesis helps eliminate bias in research. Researchers approach their study without preconceived notions about the outcome, ensuring that the results are based on the data collected rather than personal beliefs or expectations.

3. Framework for Statistical Testing

The null hypothesis provides a structured framework for conducting statistical tests. It is essential for calculating p-values and test statistics, which determine whether the observed data are significantly different from what would be expected under the null hypothesis. This framework allows for a standardized approach to testing hypotheses across various fields of study.

4. Facilitates Decision Making

The null hypothesis facilitates decision-making in research by providing clear criteria for accepting or rejecting it. If the data provide sufficient evidence to reject the null hypothesis, researchers can conclude that there is a statistically significant effect or difference. This decision-making process is critical in advancing scientific knowledge and understanding.

5. Controls Type I and Type II Errors

The null hypothesis plays a crucial role in controlling Type I and Type II errors in hypothesis testing. A Type I error occurs when the null hypothesis is incorrectly rejected (a false positive), while a Type II error happens when the null hypothesis is incorrectly accepted (a false negative). By defining the null hypothesis, researchers can set significance levels (e.g., alpha level) to manage the risk of these errors.

When is the Null Hypothesis Rejected?

Rejecting the null hypothesis is a critical step in the process of hypothesis testing. The decision to reject the null hypothesis is based on statistical evidence derived from the data collected in a study. Below are the key factors that determine when the null hypothesis is rejected:

The p-value is a measure of the probability that the observed data (or something more extreme) would occur if the null hypothesis were true. The null hypothesis is rejected if the p-value is less than or equal to the predetermined significance level (?).

• Significance Level (?): This is the threshold set by the researcher, commonly 0.05 (5%). If the p-value ? 0.05, the null hypothesis is rejected.
• If a p-value of 0.03 is obtained and the significance level is 0.05, the null hypothesis is rejected.

2. Test Statistic

The test statistic is a standardized value calculated from sample data during a hypothesis test. It measures the degree to which the sample data differ from the null hypothesis. The decision to reject the null hypothesis depends on whether the test statistic falls within the critical region.

• Critical Region: This is determined by the significance level and the distribution of the test statistic (e.g., Z-distribution, t-distribution).
• In a two-tailed test with ? = 0.05, the critical region for a Z-test might be Z < -1.96 or Z > 1.96. If the test statistic is 2.10, the null hypothesis is rejected.

3. Confidence Intervals

Confidence intervals provide a range of values that are likely to contain the population parameter. If the confidence interval does not include the value specified by the null hypothesis, the null hypothesis is rejected.

• If a 95% confidence interval for the mean difference between two groups is (2.5, 5.0) and the null hypothesis states that the mean difference is 0, the null hypothesis is rejected.

4. Effect Size

Effect size measures the magnitude of the difference between groups or the strength of a relationship between variables. While not a direct criterion for rejecting the null hypothesis, a substantial effect size can support the decision to reject the null hypothesis when combined with a significant p-value.

Null Hypothesis vs. Alternative Hypothesis

How to Write a Null Hypothesis

Writing a null hypothesis is a crucial step in designing a scientific study or experiment. The null hypothesis (H0) serves as a starting point for statistical testing and represents a statement of no effect or no difference. Here’s a step-by-step guide on how to write a null hypothesis:

1. Identify the Research Question

Start by clearly defining the research question you want to investigate. Understand what you are testing and what you expect to find.

• Example Research Question: Does a new medication reduce blood pressure more effectively than an existing medication?

2. Determine the Variables

Identify the independent and dependent variables in your study.

• Independent Variable: The variable that is manipulated or categorized (e.g., type of medication).
• Dependent Variable: The variable that is measured or observed (e.g., blood pressure).

3. State the Null Hypothesis Clearly

The null hypothesis should assert that there is no effect, no difference, or no relationship between the variables. It is usually written as a statement of equality or no change.

• Format: “There is no [effect/difference/relationship] in [dependent variable] between [independent variable groups].”
• Example: “There is no difference in blood pressure reduction between the new medication and the existing medication.”

4. Use Proper Symbols and Notation

In formal scientific writing, use symbols and proper notation to represent the null hypothesis.

• Here, ?1 represents the mean blood pressure reduction for the new medication, and ?2 represents the mean blood pressure reduction for the existing medication.

Why is the null hypothesis important?

The null hypothesis is crucial as it provides a baseline for comparison and allows researchers to test the significance of their findings.

How do you state a null hypothesis?

A null hypothesis is stated as no effect or no difference, typically in the form “There is no [effect/difference] between [groups/variables].”

What is the alternative hypothesis?

The alternative hypothesis (H1) suggests that there is an effect or difference between variables, opposing the null hypothesis.

What does it mean to reject the null hypothesis?

Rejecting the null hypothesis means the data provides sufficient evidence to support the alternative hypothesis, indicating a significant effect or difference.

What is a p-value?

A p-value measures the probability that the observed data would occur if the null hypothesis were true. Low p-values indicate strong evidence against the null hypothesis.

What is a Type I error?

A Type I error occurs when the null hypothesis is incorrectly rejected, meaning a false positive result is concluded.

What is a Type II error?

A Type II error happens when the null hypothesis is incorrectly accepted, meaning a false negative result is concluded.

How do you choose a significance level (?)?

The significance level, often set at 0.05, is chosen based on the acceptable risk of making a Type I error in the context of the study.

Can the null hypothesis be proven true?

No, the null hypothesis can only be rejected or not rejected. Failing to reject it does not prove it true, only that there is not enough evidence against it.

What is the role of sample size in hypothesis testing?

Larger sample sizes increase the test’s power, reducing the risk of Type II errors and making it easier to detect a true effect.

Text prompt

• Instructive
• Professional

10 Examples of Public speaking

20 Examples of Gas lighting

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.1 - setting the hypotheses: examples.

A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.

Example 10.2: Hypotheses with One Sample of One Categorical Variable Section  

About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.

• Research Question : Are artists more likely to be left-handed than people found in the general population?
• Response Variable : Classification of the student as either right-handed or left-handed

State Null and Alternative Hypotheses

• Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
• Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.

Example 10.3: Hypotheses with One Sample of One Measurement Variable Section  

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.

• Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
• Response Variable : dosage of the active ingredient found by a chemical assay.
• Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
• Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.

Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section  

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.

• Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
• Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
• Explanatory (Grouping) Variable: Sex
• Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
• Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.

Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section  

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.

• Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
• Response Variable : Weight loss (pounds)
• Explanatory (Grouping) Variable : Type of diet
• Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
• Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.

Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section  

• Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
• Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
• Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
• Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.

This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.

Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section  

• Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
• Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
• Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
• Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.

Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section  

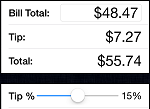
• Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
• Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
• Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
• Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.